Нейрокомпьютинг: история, состояние, перспективы

Теория нейронных сетей привлекает сегодня внимание многих исследователей. С одной стороны, интерес к нейросетевым моделям вызван желанием понять принципы работы нервной системы, с другой стороны, с помощью таких моделей ученые рассчитывают смоделировать поразительные по своей эффективности процессы обработки информации, свойственные живым существам. В нашей статье речь пойдет о направлении в теории нейронных сетей, получившем название нейрокомпьютинг (neurocomputing). Основные положения данной статьи взяты из работ .

Нейрокомпьютинг - это технология создания систем обработки информации (например, нейронных сетей), которые способны автономно генерировать методы, правила и алгоритмы обработки в виде адаптивного ответа в условиях функционирования в конкретной информационной среде. Нейрокомпьютинг представляет собой фундаментально новый подход, а рассматриваемые в рамках этого подхода системы обработки информации существенно отличаются от упомянутых ранее систем и методов. Данная технология охватывает параллельные, распределенные, адаптивные системы обработки информации, способные «учиться» обрабатывать информацию, действуя в информационной среде. Таким образом, нейрокомпьютинг можно рассматривать как перспективную альтернативу программируемым вычислениям, по крайней мере, в тех областях, где его удается применять.

Новый подход не требует готовых алгоритмов и правил обработки - система должна «уметь» вырабатывать правила и модифицировать их в процессе решения конкретных задач обработки информации. Для многих задач, где такие алгоритмы неизвестны, или же известны, но требуют значительных затрат на разработку ПО (например при обработке зрительной и слуховой информации, распознавании образов, анализе данных, управлении), нейрокомпьютинг дает эффективные, легко и быстро реализуемые параллельные методы решения. Заметим, что представляет интерес также и обратная задача: анализируя обученную систему, определить разработанный ею алгоритм решения задачи.

Информационные структуры, которые в первую очередь входят в область нейрокомпьютинга - это нейронные сети, хотя иногда рассматриваются и другие классы адаптивных структур обработки информации: обучающиеся автоматы; генетические обучающиеся системы; системы запоминания информации, адаптирующиеся к конкретным данным; имитационные системы, работающие по принципу «отжига»; ассоциативные системы памяти; обучающиеся системы, построенные на принципах нечеткой логики.

Модельная нейронная сеть (artificial neural network) - это параллельная система обработки информации, состоящая из обрабатывающих элементов (нейронов), которые локально выполняют операции над поступающими сигналами и могут обладать локальной памятью. Элементы связаны друг с другом однонаправленными каналами передачи сигналов. Каждый обрабатывающий элемент имеет единственный выход, иногда разветвляющийся на несколько каналов (связей), по каждому из которых передается один и тот же выходной (результирующий) сигнал обрабатывающего элемента. Правила образования результирующего сигнала (правила обработки информации внутри элемента) могут варьироваться в широких пределах, важно лишь, чтобы обработка была локальной. Это означает, что обработка должна зависеть от текущих значений входных сигналов, поступающих на элемент через связи и от значений, хранящихся в локальной памяти элемента.

Считается, что теория нейронных сетей, как научное направление, впервые была обозначена в классической работе МакКаллока и Питтса 1943 г., в которой утверждалось, что, в принципе, любую арифметическую или логическую функцию можно реализовать с помощью простой нейронной сети. В 1958 г. Фрэнк Розенблатт придумал нейронную сеть, названную перцептроном, и построил первый нейрокомпьютер Марк-1 . Перцептрон был предназначен для классификации объектов. На этапе обучения «учитель» сообщает перцептрону к какому классу принадлежит предъявленный объект. Обученный перцептрон способен классифицировать объекты, в том числе не использовавшиеся при обучении, делая при этом очень мало ошибок.

Новый взлет теории нейронных сетей начался в 1983-1986 г. г. При этом важную роль сыграли работы группы PDP (Parallel Distributed Processing) . В них рассматривались нейронные сети, названные многослойными перцептронами, которые оказались весьма эффективными для решения задач распознавания, управления и предсказания. (Многослойные перцептроны занимают ведущее положение, как по разнообразию возможностей использования, так и по количеству успешно решенных прикладных задач .)

 Многослойный перцептрон

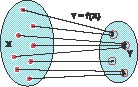Рис.1. Функция f ставит в соответствие каждому вектору X из m - мерного пространства некоторый вектор Y из p-мерного пространства

Рассмотрим функцию Y=f(X), которая ставит в соответствие m-мерному вектору X некоторый p-мерный вектор Y (Рис. 1). Например, в задаче классификации вектор X- это классифицируемый объект, характеризуемый m признаками; вектор Y, состоящий из одной единицы и остальных нулей, является индикатором класса, к которому принадлежит вектор X (позиция единицы означает номер класса). Функция f ставит в соответствие каждому объекту тот класс, к которому он принадлежит.

Предположим, нам нужно найти функцию f. Воспользуемся методом обучения на примерах. Предположим, что имеется репрезентативная выборка векторов Xi, для которых известно значение функции Yi=f(Xi). Набор пар (Xi,Yi) будем называть обучающей выборкой. Рассмотрим теперь нейронную сеть, называемую многослойным перцептроном, определив, как устроены элементы сети («нейроны»), какова архитектура связей между элементами и по каким правилам будет происходить обучение сети.

Элемент сети функционирует в дискретном времени и на основании поступивших сигналов формирует результирующий сигнал. Элемент имеет несколько входов, каждому из которых предписан определенный «вес». Сигналы, поступающие по входам, суммируются с учетом соответствующих весов, и суммарный сигнал сравнивается с порогом срабатывания. Если суммарный сигнал меньше порога, то сигнал на выходе элемента близок или равен нулю, в противном случае сигнал близок к единице.

Каждый элемент входного слоя имеет один вход (с весом 1), по которому поступает соответствующая компонента вектора X. Каждый элемент скрытого слоя получает сигналы ото всех элементов входного слоя. Тем самым, элемент скрытого слоя имеет m входов, связывающих его с элементами входного слоя. Связи от элементов входного слоя к элементам скрытого слоя характеризуются матрицей «весов» связей w1, компоненты которой определяют величину эффективности связи. Каждый элемент выходного слоя получает сигналы ото всех элементов скрытого слоя. Таким образом, подавая на входной слой сети вектор X, мы получаем вектор активности элементов скрытого слоя и затем вектор Y на элементах выходного слоя. Результат работы сети зависит от числовых значений весов связей между элементами.

Обучение сети состоит в правильном выборе весов связей между элементами. Выбираются такие веса связей, чтобы суммарная среднеквадратичная ошибка для элементов обучающей выборки была минимальной. Достичь этого можно разными методами . После обучения перцептрона проводится процедура тестирования, позволяющая оценить результаты работы. Для этого обучающую выборку обычно делят на две части. Одна часть используется для обучения, а другая, для которой известен результат, задействована в процессе тестирования. Процент правильных результатов работы сети на этапе тестирования является показателем качества работы перцептрона.

Надо сказать, что для очень многих практических задач удается достичь на удивление высокого качества работы сети (порядка 95% и выше). Существует ряд математических теорем , обосновывающих возможность применения многослойных перцептронов для аппроксимации достаточно широкого класса функций f.

Проиллюстрируем применение многослойных перцептронов на примере решения задачи сжатия информации. Такая необходимость часто возникает в различных приложениях, в частности, при распознавании образов существует этап предобработки, когда исходные данные представляются в компактной, удобной форме. Результаты этого этапа зачастую определяют успех в решении задачи распознавания.

Популярный метод сжатия информации был предложен в 1987 г. G.Cottrell, P.Munro, D.Zipser . Рассмотрим трехслойный перцептрон, у которого число элементов входного и выходного слоев одинаково, а число элементов скрытого слоя значительно меньше. Предположим, что в результате обучения на примерах (на векторах обучающей выборки) перцептрон может воспроизводить на выходе тот же самый вектор X, который подается на входной слой перцептрона. Такой перцептрон автоматически осуществляет сжатие информации: на элементах скрытого слоя возникает представление каждого вектора, которое значительно короче, чем длина вектора, подаваемого на вход. Предположим, что некоторый набор векторов нужно передавать по линии связи, предварительно сжимая информацию и тем самым уменьшая число каналов, необходимых для ее передачи. Поместим на одном конце линии входной и скрытый слои перцептрона, а результат работы элементов скрытого слоя (короткие векторы) будем передавать по линии связи. На другом конце линии поместим копию скрытого слоя и выходной слой, тогда переданный короткий вектор с элементов скрытого слоя перейдет на элементы выходного слоя, где будет воспроизведен исходный вектор (декомпрессия).