«Все любят разгадывать других, но никто не любит быть разгаданным» – эти слова французского писателя Франсуа Ларошфуко как нельзя лучше отражают сущность современной криптологии как соревнования методов криптографии и криптоанализа. Появление новых криптографических алгоритмов приводит к разработке способов их взлома. Результатом возникновения каждого нового метода криптоанализа является пересмотр оценок безопасности шифров, что в свою очередь влечет за собой необходимость создания более стойких шифров.
История криптологии – науки, объединяющей криптографию и криптоанализ, – насчитывает многие века, однако особенно интенсивно эта область знаний начала развиваться с наступлением компьютерной эры. В научной криптологии взлом шифра не обязательно подразумевает обнаружение способа, применимого на практике для восстановления открытого текста по перехваченному зашифрованному сообщению. Под взломом понимается лишь подтверждение наличия уязвимости криптоалгоритма, свидетельствующее, что свойства шифра не соответствуют заявленным характеристикам.
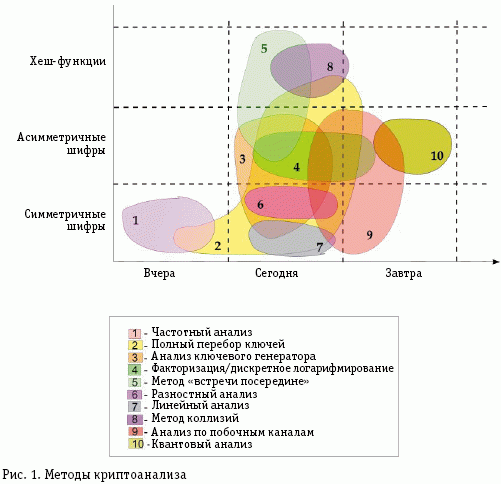
За два последних десятилетия резко возросло число открытых работ по криптоанализу, который становится одной из наиболее активно развивающихся областей исследований. Появился целый арсенал математических методов, представляющих интерес для криптоаналитика. Кроме того, повышение производительности вычислительной техники сделало возможными такие типы атак, которые раньше были неосуществимы. На рисунке изображена диаграмма, в которой методы криптоанализа систематизированы по времени их появления и применимости для взлома различных категорий криптосистем.
Частотный анализ
На протяжении веков дешифрованию криптограмм помогает частотный анализ появления отдельных символов и их сочетаний. Идея этого метода хорошо известна любителям детективов по рассказу Артура Конан Дойля «Пляшущие человечки». Вероятность появления отдельных букв, а также их порядок в словах и фразах естественного языка подчиняются задокументированным статистическим закономерностям: например, пара стоящих рядом букв «ся» в русском языке более вероятна, чем «цы», а «оь» не встречается никогда. Анализируя достаточно длинный текст, зашифрованный методом замены, можно по частотам появления символов произвести обратную замену и восстановить исходный текст.
Частотный метод породил требование равномерного распределения символов в шифртексте. Сегодня принципы частотного анализа широко применяются в программах по подбору паролей и позволяют на несколько порядков сократить время поиска.
Метод полного перебора
Возможность вскрывать шифры методом перебора ключей появилась у криптоаналитиков с распространением высокопроизводительной вычислительной техники.
При осуществлении попытки атаки на основе только шифртекста требуется анализировать выходные данные алгоритма и проверять их «осмысленность». В случае когда в качестве объекта шифрования выступает графический файл или программа, задача определения «осмысленности» выходных данных становится очень трудной. Если же известно, что открытый текст представляет собой предложение на естественном языке, проанализировать результат и опознать успешный исход дешифрования сравнительно несложно, тем более что криптоаналитик зачастую располагает некоторой априорной информацией о содержании сообщения. Задачу выделения осмысленного текста, то есть определения факта правильной дешифрации, решают при помощи ЭВМ с использованием теоретических положений, разработанных в конце XIX века выдающимся русским математиком А.А. Марковым, – так называемых «цепей Маркова».
Атаки с использованием известного или подобранного открытого текста встречаются чаще, чем можно подумать. В среде криптоаналитиков нельзя назвать неслыханными факты добычи открытого текста шифрованного сообщения или подкупа лица, которое должно будет зашифровать избранное сообщение. Предположим, злоумышленнику известна одна или несколько пар «открытый текст – шифртекст». Примем проверку одного варианта ключа k, принадлежащего множеству K, за одну операцию. Тогда полный перебор ключей потребует |K| операций для детерминированной схемы шифрования (схемы, в которой шифрование открытого текста x на ключе k приводит только к одному возможному варианту шифртекста y). Если в качестве оценки трудоемкости метода взять математическое ожидание случайной величины, соответствующей числу опробований до момента обнаружения использованного ключа, то мы получим |K|/2 операций. Кроме того, алгоритм полного перебора допускает распараллеливание, что позволяет значительно ускорить нахождение ключа.
Атака по ключам
Одной из причин ненадежности криптосистем является использование слабых ключей. Фундаментальное допущение криптоанализа, которое впервые сформулировал Огюст Кирхгоф, состоит в том, что секретность сообщения всецело зависит от ключа: механизм шифрования, кроме ключа, известен противнику. Секретность алгоритма не является большим препятствием – для определения типа программно реализованного криптографического алгоритма требуется лишь несколько дней инженерного анализа исполняемого кода. «Слабый ключ» – это ключ, не обеспечивающий достаточного уровня защиты или использующий в шифровании закономерности, которые могут быть выявлены. Алгоритм шифрования не должен иметь слабых ключей. Если это невозможно, то количество слабых ключей должно быть минимальным, чтобы уменьшить вероятность случайного выбора одного из них; все слабые ключи должны быть известны заранее, чтобы их можно было отбраковать в процессе создания ключа.
Генераторы случайных чисел – еще один источник угрозы для стойкости криптосистемы. Если для генерации ключей используется криптографический слабый алгоритм, то независимо от используемого шифра вся система будет нестойкой. Качественный ключ, предназначенный для использования в рамках симметричной криптосистемы, представляет собой случайный двоичный набор. Если требуется ключ разрядностью n , то в процессе его генерации с одинаковой вероятностью должен получаться любой из 2n возможных вариантов. Генерация ключей для асимметричных криптосистем – процедура более сложная, так как ключи, применяемые в таких системах, должны обладать определенными математическими свойствами. Например, в случае системы RSA модуль шифрования представляет собой произведение двух больших простых чисел.
Криптоанализ симметричных шифров
Наибольший прогресс в разработке методов раскрытия блочных шифров был достигнут в самом конце ХХ века, и связан он с появлением двух методов – разностного, или дифференциального, криптоанализа и линейного криптоанализа.
Метод разностного анализа сочетает в себе идею общей линейной структуры с применением вероятностно-статистических методов исследования. Этот метод относится к атакам по выбранному открытому тексту. Хотя Дональд Копперсмит утверждает, что разностный криптоанализ был известен команде разработчиков алгоритма DES (Data Encryption Standard) еще в начале 70-х годов, официальной датой появления этого метода считается 1990 год, а первенство в разработке признано за израильскими математиками Эли Бихамом и Ади Шамиром. Разностный метод основан на использовании неравновероятности в распределении значений разности двух шифртекстов, полученных из пары открытых текстов, имеющих некоторую фиксированную разность. Возникновение этого метода криптоанализа привело к появлению требования на равномерность распределения разности шифртекстов, на соответствие которому шифры проверялись на известных конкурсах, таких как AES и NESSIE. Отметим, что разностный анализ применим и для взлома хеш-функций.
Подобно разностному анализу, линейный анализ является комбинированным методом, сочетающим в себе поиск линейных статистических аналогов для уравнений шифрования и статистический анализ имеющихся открытых и шифрованных текстов, использующий также методы согласования и перебора. Этот метод исследует статистические линейные соотношения между отдельными координатами векторов открытого текста, соответствующего шифртекста и ключа, и использует эти соотношения для определения статистическими методами отдельных координат ключевого вектора.
Метод линейного криптоанализа позволил получить наиболее сильные результаты по раскрытию ряда итерационных систем блочного шифрования, в том числе и системы DES. Метод линейного криптоанализа в неявном виде был предложен еще в работе Шона Мерфи в 1990 году, где он успешно применялся при анализе системы блочного шифрования FEAL. В 1992 году Мицуру Мацуи формализовал этот подход, а позже успешно применил его к анализу криптоалгоритма DES. В 2001 году в США на смену DES и Triple DES пришел новый стандарт AES (Advanced Encryption Standard), действующий и по сей день.
Криптоанализ асимметричных шифров
Практически все используемые алгоритмы асимметричной криптографии основаны на задачах факторизации (например, известная криптосистема RSA) и дискретного логарифмирования в различных алгебраических структурах (схема электронно-цифровой подписи Эль-Гамаля). Для криптоанализа асимметричных криптосистем можно применять универсальные методы – например, метод «встречи посередине». Другой подход заключается в решении математической задачи, положенной в основу асимметричного шифра. С того момента, как Уитфрид Диффи и Мартин Хеллман в 1976 году предложили концепцию криптографии с открытым ключом, проблемы факторизации целых чисел и дискретного логарифмирования стали объектом пристального изучения математиков всего мира. За последние годы в этой области наблюдался значительный прогресс. Подтверждением тому может служить следующий казус: в 1977 году американский криптограф Рональд Ривест заявил, что разложение на множители 125-разрядного числа потребует 40 квадриллионов лет, однако уже в 1994 году было факторизовано число, состоящее из 129 двоичных разрядов!
Наиболее эффективные сегодня алгоритмы факторизации и дискретного логарифмирования имеют уже не экспоненциальную, а субэкспоненциальную временную сложность. Это алгоритмы, использующие факторную базу. Первый субэкспоненциальный алгоритм для вычисления дискретного логарифма в простом поле Zp был предложен Леонардом Адлеманом. На практике алгоритм Адлемана оказался недостаточно эффективным; Дон Копперсмит, Эндрю Одлыжко и Ричард Шреппель предложили свою версию субэкспоненциального алгоритма дискретного логарифмирования – «COS». Алгоритм решета числового поля, предложенный Оливером Широкауэром, при p > 10100 работает эффективнее различных модификаций метода COS.
Ряд успешных атак на системы, основанные на сложности дискретного логарифмирования в конечных полях, привел к тому, что российские и американские стандарты электронной цифровой подписи (ЭЦП), которые были приняты в 1994 году и базировались на схеме Эль-Гамаля, в 2001 году были обновлены и переведены на эллиптические кривые. Схемы ЭЦП при этом остались прежними, но в качестве чисел, которыми они оперируют, теперь используются эллиптические числа – решения уравнения эллиптических кривых над указанными конечными полями. Алгоритмы, выполняющие дискретное логарифмирование на эллиптических кривых в общем случае хотя бы с субэкспоненциальной сложностью, на сегодняшний день нам неизвестны, хотя работы в этом направлении ведутся.
Криптоанализ по побочным каналам
Атаки по сторонним, или побочным, каналам используют информацию, которая может быть получена с устройства шифрования и не является при этом ни открытым текстом, ни шифртекстом. Такие атаки основаны на корреляции между значениями физических параметров, измеряемых в разные моменты во время вычислений, и внутренним состоянием вычислительного устройства, имеющим отношение к секретному ключу. Этот подход менее обобщенный, но зачастую более мощный, чем классический криптоанализ.
В последние годы количество криптографических атак, использующих слабости в реализации и размещении механизмов криптоалгоритма, резко возросло. Противник может замерять время, затрачиваемое на выполнение криптографической операции, или анализировать поведение криптографического устройства при возникновении определенных ошибок вычисления. Другой подход предполагает отслеживание энергии, потребляемой смарт-картой в процессе выполнения операций с секретным ключом (например, расшифрования или генерации подписи). Побочную информацию собрать порой несложно – сегодня выделено более десяти побочных каналов, в том числе электромагнитное излучение, ошибки в канале связи, кэш-память и световое излучение.
Нанотехнологии в криптоанализе
В 1994 году Питер Шор открыл так называемый «ограниченно-вероятностный» алгоритм факторизации, который позволяет с помощью квантового компьютера разложить на множители число за полиномиальное от размерности задачи время. Алгоритм Шора разложения чисел на множители явился главным достижением в области квантовых вычислительных алгоритмов. Именно с этого момента началось усиленное финансирование работ по созданию квантовых компьютеров.
Важно отметить, что алгоритм Шора чрезвычайно прост и довольствуется гораздо более скромным аппаратным обеспечением, чем то, которое понадобилось бы для универсального квантового компьютера. Поэтому вероятно, что квантовое устройство для разложения на множители будет построено задолго до того, как весь диапазон квантовых вычислений станет технологически осуществимым. Сегодня уже есть конкретные результаты. Так, IBM продемонстрировала работу созданного в лабораториях компании семикубитового квантового компьютера для факторизации чисел по алгоритму Шора. Хотя решенная им задача вряд ли способна поразить воображение (компьютер верно определил, что делителями числа 15 являются числа 5 и 3), это самое сложное вычисление за всю историю квантовых компьютеров.
***
Но если прогресс в области разработки новых методов взлома настолько велик, почему мы продолжаем использовать криптосистемы, стойкость которых постоянно снижается? Ведь еще во времена Второй мировой войны основоположником современной криптографии Клодом Шенноном было доказано, что существуют принципиально нераскрываемые шифры – совершенно секретные системы, в которых ключ, «накладываемый» на текст, не может использоваться повторно, а его размер больше либо равен объему текста.
Дело в том, что использование способа шифрования, получившего название «одноразовых блокнотов», в большинстве случаев оказывается слишком дорогим и неоправданным. Нет смысла бороться за устойчивость системы защиты информации к взлому ниже некоторой «фоновой» вероятности, когда на другой чаше весов оказываются такие характеристики криптосистемы, как стоимость, сложность реализации и скорость доступа к зашифрованному тексту. Выбор необходимой степени защиты – это поиск компромисса между уровнем безопасности и расходами на ее обеспечение. Таким образом, разработка новых методов криптоанализа с последующей публикацией и открытым обсуждением результатов является основным двигателем современной криптографии.
Сергей Авдошин (savdoshin@hse.ru) – зав. кафедрой управления разработкой программного обеспечения, руководитель отделения программной инженерии,
Александра Савельева (asavelieva@hse.ru) – доцент ГУ ВШЭ (Москва).
Разрядность – не панацея
На первый взгляд кажется, что с ростом мощности компьютеров разрядность ключа, достаточная для обеспечения безопасности информации против атаки методом полного перебора, будет неограниченно расти, но это не так. Существуют фундаментальные ограничения вычислительной мощности, наложенные структурой вселенной: например, скорость передачи любого сигнала не может превышать скорость распространения света в вакууме, а количество атомов во Вселенной (из которых в конечном счете состоят компьютеры) огромно, но конечно.
Предел, основанный на выделяемой Солнцем энергии. Все вычисления потребляют энергию. Мощность излучения Солнца составляет приблизительно 3,86 х 1026 Вт, таким образом, за весь свой предполагаемый период существования, 10 млрд лет, Солнце выделит около 1044 Дж. Количество вычислительных операций, которые можно осуществить с использованием всей выделяемой Солнцем энергии, равно выделяемой мощности, поделенной на количество энергии, необходимой для осуществления одной операции (всего 1073 операций). Такое количество операций потребовалось бы на взлом ключа из 73 десятичных цифр (или около 250 бит) методом прямого перебора при грубом предположении, что для проверки одного значения ключа необходима всего одна операция (на самом деле – сотни).
Предел, основанный на массе Земли. Масса Земли составляет порядка 6 х 1024 кг, масса протона – 1,6 х 1027 кг, вся Земля содержит приблизительно 4 х 1051 протонов. Сопоставим каждому протону отдельный компьютер и примем за скорость выполнения операции на таком компьютере время, за которое луч света проходит расстояние, равное диаметру этого протона, и получим, что каждый компьютер может выполнять 3 х 1025 операций в секунду. Если все эти компьютеры будут работать параллельно, их суммарное быстродействие составит 4 х 1051 + 3 х 1025 операций в секунду – 1077 операций в секунду. Возраст Вселенной приблизительно равен 3 х 1017 секунд. За весь период существования Вселенной такие гипотетические компьютеры размером с протон смогли бы выполнить 3 х 1094 операций. При описанных в предыдущем ограничении предположениях относительно количества операций, необходимых на проверку значения ключа, такое количество операций позволит взломать ключ длиной 95 десятичных цифр, или 320 бит.
Минимальный размер ключа, необходимый для защиты информации от атак злоумышленника, будет расти по мере повышения быстродействия компьютеров, тем не менее приведенные вычисления показывают, что существует возможность выбрать такую длину ключа, что атаку методом полного перебора будет провести в принципе невозможно, вне зависимости от повышения вычислительной мощности компьютеров или успехов в области классической теории алгоритмов.
Цифровая подпись. Эллиптические кривые
Научившись эффективно решать задачу разложения на множители, можно намного ускорить решение задачи логарифмирования. При этом задача дискретного логарифмирования остается вычислительно более сложной, чем задача разложения, и, если будет найден полиномиальный алгоритм ее решения, станет возможным и разложение на множители.
Автором идеи создания квантового компьютера стал физик Ричард Фейнман, который в 1958 году обнаружил, что для решения квантовых задач недостаточно объема памяти классического компьютера. Фейнман высказал мысль о том, что способ ее решения должен соответствовать природе задачи – и предложил один из вариантов квантового компьютера.
