ТРАНЗИТИВНОЕ ЗАМЫКАНИЕ

Тогда Иван является предком Федора в силу транзитивности отношения «быть предком». Транзитивное замыкание — это простая в реализации структура данных, которая конструируется в данном случае из фамильных деревьев и помогает быстро ответить на подобные вопросы. Более формально, транзитивное замыкание — это расширение или надмножество транзитивного бинарного отношения (т. е. такого отношения, что если (a,b) и (b,c) находятся в этом отношении, то (a,c) также находится в этом отношении). По сути, эта структура данных позволяет отвечать на вопросы «достижимости», такие как «существует ли путь из точки А в точку Б?». Отправной точкой в процессе (в данном случае это код T-SQL), создающем транзитивное замыкание, является ориентированный граф (пары узлов со стрелками, которые могут быть пройдены только в одном направлении).

Во многих базах данных хранятся такие графы — например, материально-технические накладные со списком пар «узел — деталь», Web-ссылки от страницы источника к целевой странице, должностная иерархия. Выходными данными являются пары узлов, для которых существует путь. Например, транзитивное замыкание входных данных вышеупомянутой накладной — это совокупность всех пар «узел — деталь», независимо от того, непосредственно они содержатся друг в друге — как булочка с джемом содержит джем, и при этом на выходе получается (булочка, джем), или не непосредственно — булочка содержит джем, джем содержит сахар, поэтому булочка содержит сахар; на выходе при этом получается (булочка, джем), (джем, сахар), (булочка, сахар).

Транзитивное замыкание графа Web-ссылок — это совокупность всех пар «начальная страница» — «целевая страница», опять-таки с прямыми или непрямыми ссылками между ними. Как только транзитивное замыкание входного графа составлено, мы легко можем определить, существует ли конкретная пара, и таким образом ответить на вопросы типа «содержит ли узел A деталь C?» и «можно ли по ссылкам попасть со страницы X на страницу Y?». Найти формальное определение транзитивного замыкания и соответствующих терминов и алгоритмов можно на Web-сайте национального института стандартов и технологии США (NIST) (http://www.nist.gov/dads/HTML/transitiveClosure.html).

В том случае когда приложение должно как можно быстрее отвечать на запросы достижимости по графу, который хранится в базе данных, нам может понадобиться составить транзитивное замыкание в базе данных. Например, представим себе ситуацию, когда к материально-технической накладной, хранящейся в базе данных, поступает множество запросов о том, содержит ли одно изделие, скажем, шоколадный пирог, а другое изделие — сахар. Можно воспользоваться T-SQL и реализовать итерационный или рекурсивный алгоритм так, чтобы каждый запрос обходил граф начиная с основного изделия в поиске компонента.

Однако тот, кто знаком с такими итерационными решениями, знает, что они обычно медленны и их использование связано с большими издержками. Вместо этого мы можем написать код T-SQL, который составляет транзитивное замыкание материально-технической накладной и создает соответствующую таблицу. Эта таблица будет содержать все пары изделий, между которыми существует путь. Как только наш код материализует транзитивное замыкание накладной, мы сможем использовать его для получения ответа на любые запросы о том, содержится ли одно изделие в другом, выполняя простой запрос с одной поисковой операцией по индексу, созданному по паре атрибутов.

Одной из смежных проблем является нахождение кратчайшего пути между двумя узлами в графе. Например, если в базе данных SQL Server хранится информация о Web-ссылках, то, возможно, приложению приходится отвечать на частые запросы о минимуме Web-ссылок, которые могут потребоваться при переходе с одной страницы на другую. Рекомендуем алгоритмы транзитивного замыкания Роберта Флойда и Стефена Вошала, часто применяемые в других вычислительных средах. Подробности можно найти на сайте http://www.nist.gov/dads, набрав в строке поиска Floyd или Warshall. Однако, несмотря на то что эти алгоритмы могут предоставить наиболее удобные программные решения для упомянутых проблем, в реляционных базах данных они не работают, поскольку не могут быть выражены в запросах SQL.

С появлением в SQL Server 2005 рекурсий для общих табличных выражений (CTE) мы можем создавать чистые T-SQL-решения проблем транзитивного замыкания и кратчайшего пути. Рассмотрим несколько примеров. Сначала представим довольно простое решение для ациклического графа, в котором ни один узел не имеет пути к самому себе. Затем исследуем более сложное решение для циклических графов, в которых уже может существовать путь узла к самому себе. Мы исходим из предположения, что читатели знакомы с рекурсивными CTE.

Ациклические графы

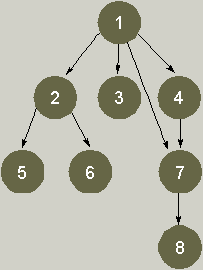
Рисунок 1. Ациклический граф

В наших примерах задействованы сценарии с Web-ссылками. Прежде чем перейти к дальнейшему изложению, следует выполнить код листинга 1, чтобы создать таблицу Links и заполнить ее данными примера. Таблица Links содержит строки для каждой Web-ссылки, в том числе два атрибута: ID страницы-источника (src_pid) и ID целевой страницы (tgt_pid). Данным соответствует ациклический граф, а это означает, что, следуя по ссылкам, никак нельзя попасть со страницы на ту же самую страницу. На рис. 1 изображен ациклический ориентированный граф, соответствующий таблице Links.

Первый пример, который мы рассмотрим, — запрос, создающий транзитивное замыкание таблицы Links. Результат показан в табл. 1, которая содержит все пары ID исходной-целевой страниц, имеющие путь от первой ко второй. В листинге 2 показано решение по этому запросу.

Во фрагменте под меткой A «якорь» CTE с именем TC возвращает из таблицы Links все пары Web-страниц (исходная, целевая), в которых на целевую страницу можно перейти непосредственно с исходной (по одной ссылке). Рекурсивный член во фрагменте B объединяет результаты предыдущего шага (имеющего в TC псевдоним P — Parent, родительский) с таблицей Links (имеющей псевдоним C — Child, дочерний), чтобы возвратить целевые страницы, на которые пользователь может перейти не непосредственно (следуя более чем по одной ссылке). Условие JOIN ищет в таблице Links строки, в которых ID исходной страницы равны ID целевой страницы предыдущего шага. В списке SELECT возвращаются ID исходных страниц шага B и ID целевых страниц шага C.

Первое инициирование работы рекурсивного выражения возвращает целевые страницы, которые отстоят на две ссылки от исходной. Второе инициирование возвращает целевые страницы, которые отстоят на три ссылки от исходной и т. д., пока рекурсивное выражение не исчерпает все связанные страницы. После этого внешний запрос делает выборку чистого списка пар исходная — целевая страница. Мы применили DISTINCT, потому что без него результат имел бы дублирующие строки, когда от исходной страницы к целевой ведет несколько путей. Если удалить DISTINCT, в результирующем наборе мы увидим две дополнительные строки. Обе пары (1, 7) и (1, 8) дублированы, так как во входном графе существуют пути 1-4-7 и непосредственно 1-7 для пары (1, 7) и пути 1-4-7-8 и 1-7-8 для пары (1, 8).

С небольшими добавлениями в CTE, как показано в листинге 3, мы также можем вычислить минимальное расстояние (кратчайший путь) между узлами этого ациклического ориентированного графа. Другими словами, минимальное число ссылок, по которым надо пройти, чтобы попасть с одной страницы на другую. В анкерном члене добавляем константу 1, которая представляет собой расстояние, поскольку якорный член возвращает непосредственную ссылку. Рекурсивный член вычисляет расстояние как родительское расстояние плюс один. Внешний запрос группирует результаты по ID исходной и целевой страниц и возвращает минимальное расстояние для каждой пары. Исполнение кода листинга 3 дает желаемый результат, который показан в табл. 2.

Имейте в виду, что граф Web-ссылок является графом с равноотстоящими узлами, т. е. расстояние между источником и целевой страницей считается одним и тем же (один щелчок кнопкой мыши), что отличается от графа с неравноотстоящими узлами, который имеет атрибут расстояния между узлами для тех случаев, когда могут быть разные расстояния для разных пар. Поэтому мы использовали в качестве расстояния между исходной и целевой Web-страницами константу 1 как в якорном члене, так и на шаге приращения в рекурсивном члене. Графы с неравноотстоящими узлами (например, карта дорог и скоростных магистралей с разными расстояниями между разными парами исходного и целевого пункта назначения) требуют небольшого изменения для кумулятивного вычисления полного расстояния. Требуется просто заменить константу 1 атрибутом, хранящим актуальное расстояние между узлами.

Циклический граф

С циклическими графами, в которых может существовать путь от узла к самому себе, обращаться намного сложнее, главным образом потому, что можно зациклиться в бесконечном обходе путей. Пример циклического графа дает Web-сайт, где можно оказаться на той же странице, с которой был начат просмотр, после переходов по нескольким ссылкам. Хитрость в обращении с циклическими графами состоит в выявлении и учете циклов, так чтобы код знал, когда прекратить обход.

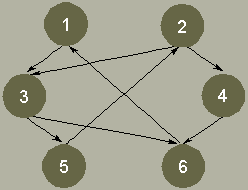
Рисунок 2. Циклический ориентированный граф

Выполним код листинга 4, чтобы заново заполнить таблицу Links графом, содержащим циклы. На рис. 2 показаны связи между Web-страницами во вновь заполненной таблице Links. Теперь таблица Links соответствует циклическому ориентированному графу.

В листинге 5 показан код, который возвращает все возможные пути и их длины в циклическом ориентированном графе. Далее мы продемонстрируем две модификации запроса, который составляет транзитивное замыкание и вычисляет кратчайшие пути между любыми двумя узлами циклического ориентированного графа. Запрос в листинге 5 обходит пути, начиная с каждой страницы как якорной, поскольку каждая страница может быть началом навигации. В процессе навигации запрос вычисляет расстояния от якорной страницы и конструирует из ID страниц пронумерованный путь, ведущий от исходной страницы к целевой. Рекурсивное выражение отфильтровывает узлы, для которых оно обнаружило цикл; распознавание цикла происходит в том случае, если ID целевой страницы уже появлялся в пронумерованном пути исходной страницы. Наше CTE распознает цикл, используя предикат LIKE в фильтре рекурсивного члена.

Исполнение кода листинга 5 дает желаемый результат, который показан в табл. 3. Возвратить транзитивное замыкание ссылок (циклический ориентированный граф), показанное в табл. 4, можно, скорректировав внешний запрос листинга 5 так, чтобы он возвращал только чистый список из ID исходных и целевых страниц. Код листинга 6 содержит два исправления кода листинга 5. Он возвращает только пары ID исходных и целевых страниц, не возвращая атрибуты расстояния и пути, и только чистый список пар, генерируя в результате актуальное транзитивное замыкание. Следует иметь в виду, что транзитивное замыкание содержит чистый список исходных и целевых элементов, имеющих путь между ними.

Наконец, код листинга 7 показывает, как возвратить кратчайшие пути (но не все возможные пути) между страницами — элементами таблицы Links, представляющей циклический ориентированный граф. В листинге 7 тело CTE совпадает с CTE в листинге 5. Внешний запрос вычисляет минимальное расстояние для каждой пары страниц и генерирует производную таблицу MD из этих данных. Затем внешний запрос объединяет все пути в MD (экземпляр TC назван AP). Условный оператор JOIN действует на основе совпадений ID исходной и целевой страниц, а расстояние из AP должно равняться минимальному расстоянию из MD. Объединение между AP и MD — это основное дополнение в код листинга 5, которое возвращает все пути. Важность оператора JOIN состоит в том, что мы получаем только пары страниц с минимальным расстоянием между ними плюс актуальные пути. Выполним код листинга 7, чтобы получить результат, показанный в табл. 5.

Транзитивное замыкание и рекурсивные CTE

Мы рассмотрели способы использования новых возможностей рекурсивных запросов SQL Server 2005 и создания коротких ANSI-совместимых решений на базе множеств для задач составления транзитивного замыкания и поиска кратчайшего пути. Описанную выше технику можно реализовать в приложениях, которые управляют запросами к иерархической информации, например в материально-технической накладной, и в приложениях, в которых встречаются вопросы «достижимости», например, для дорожных систем. Решения для ациклических графов весьма просты и основаны на обходе одного уровня за один раз. В решениях для циклических графов используются похожие обходы уровней, но задействована еще и техника распознавания циклов, прекращающая процесс обхода в тот момент, когда обнаружен цикл. Используя технику, которую мы продемонстрировали в этой статье, можно быстро получать ответы на запросы о существовании пути между двумя узлами графа и о нахождении кратчайшего пути.

Ицик Бен-Ган - Cтарший преподаватель на курсах по SQL Server в колледже Hi-Tech в Израиле. Имеет сертификаты MCDBA, MCSE+I, MCSD, MCT и SQL Server MVP. Глава израильской группы пользователей SQL Server. itzikb@hi-tech.co.il

Любор Колар - Менеджер группы в подразделении SQL Server в Microsoft. Его группа отвечает за оптимизацию запросов, исполнение и другие аспекты функционирования реляционного хранилища SQL Server. lubork@msn.com

От редакции: представленные в этой статье решения требуют установки SQL Server 2005 Beta 1 или более поздних версий. Решения разрабатывались и тестировались на предварительной версии SQL Server 2005 Beta 2 Ициком Бен-Ганом и Любором Коларом.