Третье конкурсное задание для тех, кто намерен бороться за Национальную премию в области компьютерных аудиовизуальных искусств и технологий «Эвридика» («Мир ПК», б№1/02, с.71, б№2/02, с.58).
Мы уже попробовали силы в растровой и 3D-графике, а теперь обратим свои взоры на один из самых проторенных путей – программирование мультимедиа, а в частности – на обработку аудиосигналов. Исторически так сложилось, что методы обработки сигналов развивались еще задолго до появления первых радиоэлектронных устройств. И до появления ПК мировое сообщество уже обладало внушительным багажом знаний и набором математических абстракций, помогающих более четко представлять природу колебательных систем и, в частности, звуковых колебаний. Большинство разработчиков ПО сейчас, как правило, используют проверенные временем методы анализа звуковых волн. Однако их рабочие места до сих пор не оборудованы надежными средствами распознавания речевого ввода, гибкими и реалистичными синтезаторами речи, переводчиками с голосовым вводом - выводом и т. д. И поскольку решены далеко не все проблемы, здесь широкий простор для творчества. Поддержим и мы поиски в этой области, начав с решения далеко не самой сложной задачи: реализации алгоритма преобразования Фурье для анализа аудиосигнала.
Итак, наше задание: написать программу на языке программирования Java, способную загружать аудиофайлы, производить их спектральный анализ с помощью преобразования Фурье, желательно быстрого, и выводить спектральную характеристику в графическом виде.
У вас не должно возникнуть каких-либо затруднений при составлении алгоритма. Литературы, где описаны преобразования Фурье, более чем достаточно, и в Интернете можно найти большое количество исходных текстов, реализующих этот алгоритм (правда, не на языке Java). Вам остается всего лишь собрать нужную информацию, преобразовать ее и написать качественное приложение. Оцениваться будут и скорость обработки, и широта функциональных возможностей программы, и качество анализа.
|
|
| Рис. 1 |
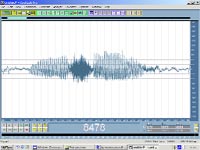
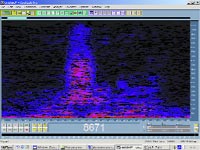
Для примера приведу изображение огибающей амплитуды и ее графика спектральной функции в аудиоредакторе Cool Edit Pro (рис.1), чтобы вы увидели, на что все это может быть похоже.
По горизонтали отложена временная ось, по вертикали частотная, а степень присутствия определенной частоты в пространстве время – частота определяется интенсивностью какого-либо цвета, в частности красного.
«Почему преобразование Фурье? – может возникнуть вопрос у тех, кто впервые столкнулся с подобной задачей программирования и численными методами анализа. – Нельзя ли выполнить анализ непосредственно огибающей интенсивности звукового сигнала?»
|
| Рис. 2 |
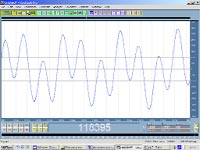
Чтобы расставить все точки над i, рассмотрим такой довольно тривиальный случай. С помощью генератора тона Cool Edit Pro синтезируем какой-нибудь комплексный сигнал из основного тона и его гармоники (рис. 2).
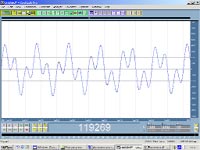
Мы получим некий гармонический сигнал определенной формы. Структура его достаточно информативна, и потому возникает соблазн провести анализ по огибающей. Если слегка модифицировать пример и немножко сместить фазу гармоники (рис. 3), то графическое изображение огибающей значительно изменится, а звучание останется прежним.
|
| Рис. 3 |
Следовательно, по форме огибающей амплитуды сигнала практически невозможно проанализировать тон звука, а кроме того, фаза составляющих звуковой волны не влияет на звучание. Значит, нам не остается ничего другого, кроме как обратиться к методам частотного анализа, которые вполне успешно используют уже не один десяток лет.
Преобразование Фурье
Итак, с чего все начиналось и почему интеграл Фурье? Дело было так: сначала математики выделили некую субстанцию, называемую рядами, и обнаружили множество интереснейших свойств, в частности, что отдельные виды рядов описывают реальные процессы. Этой особенностью обладают функциональные ряды. Например, такой
где an, bn(n=1,2,...) – коэффициенты, называется тригонометрическим. Он состоит из бесконечного множества периодических функций, где n – длительность периодического сигнала, т. е. наш ряд – набор волн с разными частотами, а коэффициенты – их амплитуды.
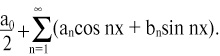
В обобщенном виде такой ряд записывается как
Если его коэффициенты можно определить через функцию f(x) по формулам
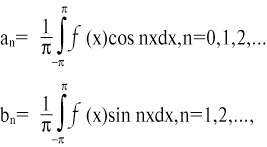
то мы получим ряд Фурье для функции f(x), где an, bn – коэффициенты Фурье.
Тогда функция f(x) будет представима в виде суммы сходящегося тригонометрического ряда.
Следовательно, мы можем взять произвольную периодическую функцию с периодом 2о?, интегрируемую на отрезке [-о?,о?], и разложить ее на множество синусоидальных составляющих – на гармоники.
А для периодических функций с произвольным периодом l формулы Фурье примут вид:
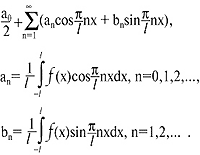
Определив функцию f(x), получим интеграл, или обратное преобразование Фурье, в комплексном виде:
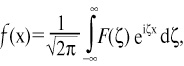
где н? – частота сигнала. Значит, прямое преобразование Фурье:
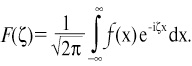
Так связываются частотные и временные характеристики некой функции. А поскольку в реальных условиях обычно приходится иметь дело с заданными отрезками времени, в канонической форме для преобразования Фурье в качестве верхнего предела интегрирования берется текущее время, а нижний предел интегрирования можно определить равным начальному моменту времени.
И тогда в нашем случае спектр частот будет определяться так:
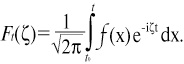
Впрочем, и здесь периодичность процесса проявляется лишь со временем, когда прорисовываются его характерные черты. Текущий спектр отражает именно такое развитие процесса.
Значит, чем более длительное время будет отслеживаться процесс колебаний, тем выше будет точность вычисления спектра.
Если рассмотреть, например, синусоидальные колебания определенной частоты, то мы увидим, как при увеличении времени наблюдения от нуля до бесконечности спектральная функция постепенно преобразуется из равномерной в функцию сначала с одним ярко выраженным пиком. С приближением к бесконечности она превратится в дискретную спектральную линию, расположенную на частоте вычисляемой синусоиды. Собственно, именно поэтому текущий спектр не подходит для полного анализа естественных звуковых колебаний, характер которых резко изменяется на кратчайших временны/х промежутках. Таким образом, было введено такое понятие, как мгновенный спектр, который определяет спектр того отрезка процесса (длительностью DТ), который непосредственно предшествовал данному моменту времени t:
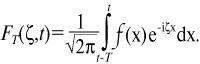
В данной формуле задается интервал интегрирования постоянной длины, но переменный по времени.
Так от абстрактных математических понятий мы пришли к конкретной формуле для определения мгновенного спектра, востребованной сегодня в области обработки звука.
Если обобщить сказанное, то для решения поставленной нами задачи нужно сделать следующее:
- взять частоту f0 условно единичной амплитуды;
- нормировать исследуемый сигнал по амплитуде;
- начиная с определенного момента t0 с шагом н?t (чем меньше шаг, тем точнее отсчет) следует перемножить отсчеты синусоиды и исследуемого сигнала в текущий момент времени, а затем полученные результаты суммировать с накоплением;
- при достижении конца исследуемого отрезка времени н?t разделить накопленную сумму на общее число отсчетов и полученный результат вывести графически. Результатом является вклад вычисляемой частоты в исследуемой функции в данной точке графика;
- повторить описанный выше процесс для каждой частоты, а затем для всех вычисляемых отрезков времени.
На практике обычно используется быстрое преобразование Фурье, но, впрочем, это относится уже к области оптимизации, поэтому оставим ее решение нашим конкурсантам.
Java Audio API
Для работы со звуком в Java предусмотрена отдельная библиотека Audio API, условно подразделяемая на Sampled, MIDI и SPI – Service Provider Interfaces.
Первая из них обрабатывает оцифрованный звук, вторая взаимодействует с MIDI-инструментами и синтезатором, а третья представляет собой средства расширения возможностей Sound API. Но здесь мы будем рассматривать только работу с оцифрованным звуком, т. е. Sampled API.
Начнем с того, что в Java можно работать с такими форматами, как WAVE, AIFF, AU и SND, применяя два подхода: упрощенный, посредством интерфейса AudioClip, и буферизованный, посредством интерфейса SourceDataLine. Первый механизм встроен в класс Applet и позволяет проигрывать любой аудиофайл всего двумя строками кода: в одной создается экземпляр класса AudioClip, конструктору которого в качестве параметра задается имя проигрываемого файла, в другой вызывается метод проигрывания аудиофайла из созданного класса.
AudioClip clip = newAudioClip(new URL(б?sound.wavб?)); clip.play();
Однако нужно получить доступ к внутренней структуре файла, и потому в нашей задаче используем более сложный метод – буферизованный вывод.
Вообще-то Sampled API в Java держится на трех китах: Format (внутреннее представление данных), Mixer (средства композиции) и Line (канал). Есть еще и четвертый, вспомогательный, – класс AudioSystem, содержащий большинство методов управления данными. Так что вся работа со звуком в Java заключается в следующем: создаем каналы ввода-вывода, загружаем данные во внутренний формат и производим действия над ними (микширование и вывод, алгоритмическая обработка, конвертирование из одного формата в другой и пр.).
Внутренний формат определяется классом AudioFormat, где должно содержаться множество параметров, которые требуется учитывать при обработке файла. Так, в этом классе должна находиться информация о частоте дискретизации (sampleRate), аппроксимации (sampleSize), числе каналов (channels, моно и стерео), знаковое или беззнаковое представление чисел (signed) и порядок расположения байтов в числе (bigEndian). Без знания этих параметров вы не сможете корректно манипулировать буфером аудиоданных. Чтобы сформировать полную структуру класса AudioFormat, нужно получить все данные из звукового файла. Это можно сделать с помощью класса AudioInputStream, являющегося расширением стандартного класса Java InputStream со всеми вытекающими отсюда последствиями. Нам же придется читать массивы байт из этого класса и записывать их в канал вывода в виде класса SourceDataLine. Ну и как вы увидите в примере, статические методы класса AudioSystem являются востребованными во множестве операций взаимодействия между классами Sampled API.
Действительно, Sampled API содержит несколько десятков классов, разделенных на группы. Каналы ввода-вывода также имеют по нескольку реализаций, из числа которых и выбираются наиболее подходящие.
А теперь вкратце посмотрим, как можно получить доступ к внутренним данным аудиофайла и провести их модификацию:
import javax.sound.sampled.*;
import java.io.*;
class PlayAudioLine{
PlayAudioLine(String s){
play(s);
}
/* определяем все операции
в конструкторе класса */
public void play(String file){
SourceDataLine line = null;
AudioInputStream ais = null;
byte[] b = new byte[500];
try{
File f = new File(file);
ais = AudioSystem.getAudioInputStream(f);
/* определяем внутренний формат
данных, полученный из файла */
AudioFormat af = ais.getFormat();
DataLine.Info info = new DataLine.Info
(SourceDataLine.class, af);
/* проверяем, поддерживается
ли такой формат */
if(!AudioSystem.isLineSupported(info)){
System.err.println("Line is not supported");
System.exit(0);
}
/* определяем параметры канала,
достав их из аудиофайла */
line = (SourceDataLine)AudioSystem
.getLine(info);
line.open(af);
line.start();
int num = 0;
/* в этом цикле мы получаем прямой доступ
к массиву b, содержащему значения
амплитуды аудиофайла, здесь же
демонстрируется его обработка */
while(( num = ais.read(b)) != -1){
for(int i = 0; i < 500; i++){
b[i] = (byte) (b[i] << 4);
}
}
/* выполняем проигрывание
модифицированных данных */
while(( num = ais.read(b)) != -1){
line.write(b, 0, num);
}
/* завершаем работу */
line.drain();
ais.close();
} catch(Exception e){
System.err.println(e);
}
line.stop();
line.close();
System.exit(0);
}
public static void main(String[] args){
/* определяем файл, задаваемый
по умолчанию, и метод извлечения
имени файла из первого аргумента
программы в переменную s для
передачи ее в конструктор */
String s = "startup2.wav";
if(args.length > 0) s = args[0];
new PlayAudioLine(s);
}
}
* * *
Итак, наши конкурсанты получили третье задание и краткое напутствие. В этот раз мы не балуем вас готовыми решениями, и если возникнут какие-либо вопросы по этому или предыдущим заданиям, пишите по адресу: vit3d@mail.ru.
