От машины Тьюринга к машине Мили

В предыдущей статье («Мир ПК», № 2/02, с. 150) мы подробно рассмотрели машину Тьюринга (МТ). Там же, коснувшись работы с несколькими головками, имеющими внутренние состояния, был намечен перспективный путь развития МТ — параллельный. Именно ему и посвящена настоящая статья.

Мама, дядя, который ходил

на одной ноге, — уже на двух.

Он себе вырастил или ему приделали?

К. Чуковский. От двух до пяти

Итак, мы рассмотрим, почему «потенциал параллелизма» у МТ выше, чем у машины Поста (МП). Будет построена параллельная машина, взявшая многое от МТ, но все же остающаяся отдельной абстрактной машиной (АМ). Создавая ее, мы заодно определим и реализацию МТ в результате детализации ее структуры. Поэтому можно будет «вживую» (правда, используя новую машину и процедуру перехода к ее программам от МТ-программ), а не на бумаге, увидеть результаты работы тьюринговых программ.

«Черный ящик»

Взглянем на любую абстрактную машину, а точнее, на ее управляющее устройство (УУ), с позиций «черного ящика». Первый его вариант — абстрактный «черный ящик» (АЧЯ), имеющий по одному входу и выходу. Символы внешнего алфавита поступают в АЧЯ через вход, обычно называемый входным алфавитом. А символы, изменяющие информацию на ленте, через выход, именуемый АЧЯ, выдает выходной алфавит. Причем допускается, что оба эти алфавита могут совпадать. Второй вариант, «структурный черный ящик» (СЧЯ) имеет множество таких каналов, и возможна ситуация, когда число входных-выходных каналов СЧЯ соответствует числу символов входного-выходного алфавитов АЧЯ. Тогда «ящик» на структурном уровне уже составляет основу модели параллельных процессов.

Чтобы отличить, какая из машин находится внутри «ящика», нужно вынести за его пределы головки машин, которыми следует управлять, выдавая им соответствующие символы. У каждой из машин они, как правило, свои, хотя между ними часто можно ввести соответствие с точностью до переименования. Символы, определяемые спецификой машины, принято относить ко множеству символов внутреннего алфавита машины: у машины Поста — это «стрелки», у машины Тьюринга — символы R и L. Безусловно, можно так определить абстрактную машину (например, путем объединения алфавитов), что символы внутреннего алфавита будут выдаваться через те же каналы, что и внешнего, но все же нагляднее и удобнее вводить дополнительные каналы.

Пока же вынос головки за пределы «ящика» еще не выявляет принципиальных различий между машинами. Их возможности в системе «ящик-головка» различаются лишь набором тех символов внутреннего алфавита, которые можно привести в соответствие простым переименованием. Существенными отличия между ними становятся тогда, когда учитывается некое внутреннее состояние «черного ящика» (ЧЯ). При этом становится видно, что машина Тьюринга обладает явным «встроенным» свойством отражать внутреннее состояние ЧЯ, а машина Поста — нет.

А необходимо ли вообще манипулировать информацией о таком внутреннем состоянии? Безусловно, ведь, например, от того, с каким «внутренним настроем» пожал вам сегодня руку ваш начальник, может зависеть многое! Казалось бы, обычное, «стандартное» действие, столь похожее на вчерашнее, но конечный результат может быть разным. Аналогично и с программами. В них внутреннее состояние — это дополнительный канал, не только следящий за ее работой, но и дающий информацию для управления ей. Именно поэтому и имеет смысл подавать информацию о внутреннем состоянии машины и на выход, и на вход «ящика». Кроме того, должно быть ясно, что данными о состоянии можно оперировать параллельно с данными на других каналах.

Было бы удобно, если бы символы внутренних состояний абстрактной машины формировали отдельное множество. Тогда можно было бы считать, что выходной алфавит СЧЯ — объединение множеств символов внутренних состояний и внутреннего алфавита машины (см. «Мир ПК», № 2-3/02).

Таким образом, можно сделать вывод: СЧЯ более удобен и гибок, чем АЧЯ, а из двух формальных моделей внутреннего устройства такого «ящика» наиболее естественна модель типа МТ, т. е. та, которая отражает понятие внутреннего состояния «черного ящика».

Операционный и управляющий блоки

Однако «ящик» еще нужно «начинить». И здесь, особенно для МТ, изобретать почти ничего не требуется, так как структурно многое отработано на цифровых схемах. Кстати, совсем не обязательно, чтобы начинка «ящика» была «железной». Но все же лучше введем, учитывая эту информацию, еще один уровень детализации структуры «ящика». В практике проектирования дискретного устройства принято выделять его операционный (ОБ) и управляющий (УБ) блоки [1]: ОБ выполняет все действия по обработке информации, а УБ реализует алгоритм работы машины в дискретном времени с помощью элементов, составляющих ОБ.

Аналогично можно поступить и на программном уровне. Используем обычный прием формального определения программы в виде так называемой схемы программы S, где S = тройка, M — множество ячеек памяти, или просто память, A — множество операторов программы, G — управление программой [2]. В этом случае память и операторы составляют ОБ, управление — УБ. Если такой подход распространить и на абстрактные машины, то М — лента, а все остальное — управляющее устройство этих машин.

Далее разберем подробнее, что будет входить в относящуюся к ОБ и УБ машину Тьюринга и соответственно МТ-программу. Рассмотрим реализацию этих блоков, взяв за основу известные языки программирования, например Си++. Те же операции распространим по возможности и на программы для МП.

Предикаты и действия МТ

Возьмем сначала операционный блок. На этом уровне множество операторов или блоков, составляющих ОБ, можно представить двойкой , где X — множество узлов (блоков, функций и/или подпрограмм и т. п.), анализирующих символы (если говорить об АМ), Y — множество узлов, преобразующих символы. Те функции, которые входят во множество X, назовем предикатами, а те, что содержатся во множестве Y, — действиями.

В случае реализации элементов ОБ для МТ на языке Си++ ее предикат может выглядеть так:

bool xN() {sn == sj;},

где s_n — текущий символ на ленте; s_i — значение того символа, которому должен соответствовать символ на ленте.

Если символы равны, то предикат xN, где N — номер предиката и номер входного канала СЧЯ, возвратит значение «истина», а если нет — «ложь». Следует заметить, это очень важно, что предикаты по замыслу не изменяют значение памяти, т. е. информации на ленте для распараллеливания.

Функции-действия (далее — просто действия) не возвращают значений, и этот факт можно подчеркнуть на Си++ типом возвращаемого значения — void. В случае с МТ действие, изменяющее текущий символ s_n на s_k, на Си++ будет иметь следующий вид:

void yN() {sn = sk;},

а действие, перемещающее головку вправо, можно представить так:

void yN() {R;}.

Предикаты и действия для машины, адресующей ячейки ленты, примут вид:

bool xN() {s[i] == sj;},
void yN() {s[i] = sk;},

где i — индекс (адрес) ячейки на ленте, представленной массивом s.

Условимся, что для действий, как и для предикатов, N — не только обозначает их номер в ОБ, но и номер выходного канала СЧЯ.

Предикаты и действия позволяют по-иному определить инструкции МТ, поставив в соответствие любому входному символу машины предикат, а любому выходному символу — действие. Причем сам переход в следующее состояние и выполнение того или иного действия возможны только при истинном значении соответствующего предиката. Теперь все многообразие видов инструкций МТ можно свести к одному, а именно:

qi,xj,yk,ql,

где x_j — предикат, принадлежащий множеству X;

y_k — действие из множества Y;

q_i, q_l — текущее и следующее состояния машины из множества ее внутренних состояний Q соответственно.

В результате получится код программы на Си++, реализующий предикаты и действия МТ, для функции И—НЕ (листинг 1):

Это вариант программы для МТ, имеющей адресацию. Лента реализована массивом целых чисел, где нулевой и первый элементы массива s содержат входные значения функции, а второй элемент — выходное.

Выше разговор шел в основном об МТ, однако с точки зрения ОБ тип рассматриваемой машины не столь важен. В случае машины Поста предикаты и действия были бы только проще. У нее был бы один предикат, анализирующий наличие или отсутствие метки на ленте, и два или четыре действия (соответственно при наличии адресации и без нее). Из которых, например, два действия ставили бы метку и очищали ячейку, а другие два перемещали бы каретку.

Таблица переходов МТ

На уровне ОБ различия между МТ и МП пока еще не принципиальны. Иное дело при рассмотрении блока УБ. Ему нужно на каком-то языке задать алгоритм или программу работы, чтобы в соответствии с ней он выполнял запуск элементов, составляющих ОБ. В случае с МТ это будет список инструкций приведенного выше вида, а для МП его вид будет другим.

Сначала рассмотрим программу УБ для МТ. Для задачи моделирования функции И—НЕ запись алгоритма работы УБ машины Тьюринга будет следующей:

q1, x1x2, y2, q2
q2, x3, y1, q1
q2, x4, y1, q1

Это вариант для машины, адресующей ячейки памяти и имеющей две головки. Для программы, использующей внутренние состояния, на месте действий нужно поставить прочерки. И в этом случае ОБ будет состоять только из предикатов.

Теперь понятно почти полное соответствие приведенной программы для УБ таблице переходов (ТП) структурного конечного автомата (КА) Мили, моделирующего такую же функцию И-НЕ. При этом в ТП одна инструкция УБ модифицированной МТ полностью соответствует одной строке таблицы переходов КА. Понятно также, почему модель КА абсолютно подходит в качестве модели УБ машины Тьюринга: переход от программы Тьюринга к таблице переходов КА почти очевиден и элементарен (он был рассмотрен ранее).

Мы вполне можем уменьшить количество предикатов, используя их отрицание. В этом случае программа, применившая для индикации состояния своего выхода внутренние состояния, может быть представлена так:

q1, x1x2, -, q2
q2, ^ x1, -, q1
q2, ^x2, -, q1

Здесь в качестве знака отрицания использован символ (^).

Возникает вопрос: нельзя ли для дальнейшего сокращения общего количества функций ввести параметры для предикатов и действий? Безусловно, можно, но, как показала практика, лучше смириться с тем, что легко устранить, нежели ухудшить эффективность реализации и получить проблемы с формальным определением и теорией самой абстрактной машины.

КА-машина: ОБ + УБ = (X + Y) + ТП

Приведем полный листинг программы, эквивалентной программе многоголовочной машины Тьюринга, использующей адресацию и внутренние состояния для отображения выходного значения функции И—НЕ (листинг 2).

Хотя форма исходной программы МТ и ее новая форма очень близки друг другу, последняя соответствует уже другой абстрактной машине, которую и мы назовем КА-машиной (далее — МКА). Эта абстрактная машина структурно разделена на ОБ и УБ, где ОБ состоит их двух множеств — предикатов и действий, а моделью УБ является модель КА. Отметим, что у МКА в отношении количества головок и отсутствия адресации может быть та же конструкция, что и у МТ, но все же со множеством головок и адресацией ячеек на ленте жить много легче. Кроме того, без всех этих головок было бы сложно построить параллельную модель. А как это можно сделать, используя их (по существу, каждая головка — отдельный входной канал ЧЯ), станет ясно уже на примере построения сетевой модели МКА.

Параллельные свойства КА-машины

Для МКА почти очевиден параллелизм функций, составляющих ее ОБ. При этом указание о том, какие функции могут исполняться параллельно, уже содержится в строках таблицы переходов УБ. Но если рассматривать какое-то текущее внутреннее состояние МКА, то параллельно могут запускаться все предикаты, нагружающие переходы из него во все другие состояния. И вполне возможно, так как они не изменяют содержимое ленты. А при ситуации перехода в следующее состояние наступает черед параллельной работы действий. Параллельно могут исполняться все действия, нагружающие переход в новое внутреннее состояние.

Такой вид параллелизма МКА соответствует синхронному параллелизму параллельных языков. В этом случае запуск множества операторов в параллельную работу происходит одновременно, а сам момент окончания их работы фиксируется по последнему оператору, закончившему работу (механизм, задаваемый операторами fork, join [3]).

Хотя этот вопрос и несколько выходит за рамки текущей задачи, нужно упомянуть и вариант дальнейшего расширения модели МКА. При иерархическом построении любое ее действие может представлять, в свою очередь, одну или несколько МКА и т. д. Но и в этом случае принцип синхронного параллелизма не должен и не будет нарушаться, поскольку любой уровень иерархии завершает свою работу только по окончании действий всех вложенных уровней.

Следующий тип параллелизма менее очевиден, но очень эффективен при наличии ассоциативной памяти (АП). После параллельного выполнения предикатов и формирования текущей входной ситуации, вычисленной на основе полученных от предикатов значений, можно приступить к параллельному анализу всех строк текущего состояния для нахождения единственной строки (так как автомат детерминированный), соответствующей ситуации перехода.

Таким образом, у МКА можно выделить три уровня параллелизма: параллелизм предикатов, действий и анализа дуг переходов текущего состояния.

О «спекуляциях» на предсказании переходов

Предсказание команд — одна из самых загадочных процедур, выполняемых современными процессорами. Если бы не эта проблема, то реализация программ была бы много эффективнее. И нынешние «спекулятивные вычисления» — одно из следствий непрекращающейся борьбы с решением проблемы переходов и причина разнообразных «спекуляций» на эту тему. Но при существующей архитектуре и от таких команд и от фактора их случайного расположения в теле программы пока никуда не деться, а потому приходится лишь удивляться, что еще что-то удается предсказывать [4].

В связи с этим нельзя не отметить, что работа, превращающая современный процессор в некое подобие гадалки, в МКА выполняется без всякого «мистицизма». Легко видно, что множество команд, которые нужно «предсказывать» в современном процессоре, для МКА (в данном случае это множество предикатов и действий) вычисляются однозначно на основе анализа таблицы переходов. При этом четко очерчен и объем определяемого для исполнения программного кода: нужно выбрать столько операторов, сколько находится в предикатах или действиях. В современном же процессоре это число определяется числом инструкций между операторами передачи управления. При неудачном «предсказании» выполняется лишняя работа и, кроме того, на само предсказание также тратится немалое время.

А в МКА же нет никаких предсказаний — все может быть сделано параллельно, быстро и однозначно.

Сетевая модель МКА: параллелизм множества машин Тьюринга

Рассмотренный выше синхронный параллелизм на уровне МКА — это лишь первый шаг на пути распараллеливания вычислительного процесса. Полным параллелизмом, универсальностью и адекватным отображением структуры обладает система, состоящая из множества одновременно работающих независимых и/или взаимодействующих между собой блоков («черных ящиков»). Такая структура, называемая сетью, хорошо описывается множеством абстрактных машин (МТ, МП, МКА и т. п.). В распространенной структурной классификации параллельных систем сетевая модель МКА (СМКА) соответствует множеству процессоров над общей памятью либо системам типа MIMD (Multiple Instruction — Multiple Data) или МКМД (множественный поток команд — множественный поток данных) [3]. И потому со структурной точки зрения здесь ничего нового нет. «Изюминка» кроется в формальной математической модели, выбранной для описания такой системы, в нашем случае — в автоматной сети из МКА.

Отличительных черт, которые присущи параллельной структуре, соответствующей формальной модели СМКА, не так уж много. Точнее, их фактически три: дискретное время для отдельной компоненты, единое дискретное время для всех параллельных компонент и возможность обмена информацией о внутренних состояниях отдельных МКА между собой. Дискретное время отдельной модели соответствует моментам перехода модели из одного состояния в другое. Формально его реальная длительность вообще не имеет значения — важно само его наличие. Единое дискретное время сети предполагает синхронизацию дискретных тактов компонентных автоматов сети, приводящую его текущее значение к текущему значению самого медленного компонентного автомата сети.

Обмен информацией о своих внутренних состояниях между компонентами сети не столь обязательное условие, как два приведенных выше, так как такой информацией можно обмениваться и через ленту. Но этот вид обмена не только значительно упрощает алгоритмы системы, поскольку вводит соответствующий тип синхронизации — через внутренние состояния, но и поддается хорошему теоретическому описанию (на этом основана алгебра конечных автоматов [5]).

Пример СМКА-модели

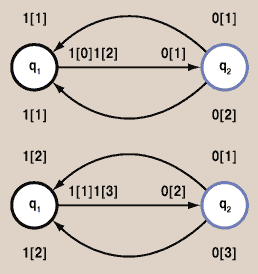
Рис. 1. СМКА-модель RS-триггера (синхронизация: память)

Сейчас мы по существу повторим описание автоматной параллельной модели RS-триггера, приведенной в работе [5], но уже в терминах моделей МКА и СМКА. Напомним, что RS-триггер — это два элемента И-НЕ, соединенных обратными связями. Модель одного элемента И-НЕ, представленного моделью МКА, мы уже рассмотрели. Граф модели триггера, которая представлена сетевой моделью СМКА, состоящей из двух моделей МКА, показан на рис. 1. В данном случае синхронизация процессов, реализующих отдельные элементы триггера, выполняется через ячейки памяти ленты. Граф и структура модели триггера, но с синхронизацией через состояния, представлены на рис. 2.

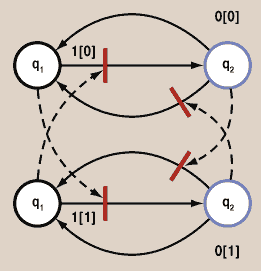
Рис. 2. СМКА-модель RS-триггера (синхронизация: состояния)

Их сравнение показывает, что синхронизация с использованием внутренних состояний упрощает модель. Скорее всего, вторая модель и работать будет быстрее, поскольку нет операций с внешней памятью. Правда, появляются операции работы с состояниями, но, во-первых, к ним доступ осуществляется по отдельным каналам, а во-вторых, это специализированный и универсальный вид операций, который может быть введен в систему команд и оптимизирован по быстродействию на аппаратном уровне.

Пример с синхронизацией через состояния убеждает нас в том, что в модель СМКА удобно ввести соответствующую операцию доступа к внутреннему состоянию отдельных (компонентных) элементов сети. Условно обозначим эту операцию запроса состояний компонентных автоматов сети как State. Она будет иметь один параметр — имя компонентного автомата сети — и возвращать строковое значение — имя текущего состояния. Программа (листинг 2), реализующая СМКА-модель RS-триггера, с учетом введенной операции может быть следующей (листинг 3).

В этой программе использовано свойство модели элемента И—НЕ находиться только в одном из двух возможных состояний. Это дает возможность ограничиться одним предикатом, анализирующим состояние «соседнего» элемента. Здесь также использованы:

• свойство предиката возвращать два значения - истинное и ложное;
• свойство таблицы переходов, оперирующей конъюнкциями входных условий.

Как видно, у МП можно увеличить количество функциональных блоков и наладить управление ими, но лишь МТ и МКА имеют внутренние состояния, позволяющие организовать синхронизацию множества параллельно работающих машин. При этом для СМКА можно создать удобную математическую теорию, а не опираться на, казалось бы, интуитивно удобные механизмы распараллеливания и синхронизации для МП (нити, потоки, семафоры и т. п.), которые все же трудно поддаются какому-то математическому описанию.

Еще раз подчеркнем, что понятие внутреннего состояния — это механизм, отсутствующий у машины Поста. И именно поэтому машина Тьюринга была выбрана в качестве основы для параллельной архитектуры. Только МТ и модель конечного автомата создают теоретически строгую, эффективно реализуемую и в то же время удобную параллельную модель. Машина Поста иногда «выигрывает» в простой последовательной работе, но для более совершенной параллельной она малопригодна.

О недостатках и достоинствах МКА

В программах для МП временной процесс смены внутренних состояний программы скрыт от программиста. Его существование следует хотя бы из того факта, что любая программа имеет время своей работы. Да и считая работу любого оператора программы «мгновенной», мы все же лукавим, поскольку и в этом случае знаем, что нужно сначала проанализировать переменные, выполнить над ними операцию и только потом присвоить полученный результат выходной переменной. В том, что это на самом деле так, легко убедиться, рассмотрев ассемблерный аналог программы или тот же хорошо многим известный пример с оператором типа «++» в параллельной среде.

Так что если нас не интересуют параллелизм и временные характеристики программы, то язык МП будет даже удобнее. В ином случае язык МП будет скрывать время и придется прибегать к ухищрениям для описания такого процесса, а это почти эквивалентно реализации другой модели в рамках имеющейся. Подобная задача может быть очень сложной (например, интерпретация конечных автоматов в рамках обычного процедурного языка).

Модель МКА отражает временные свойства программ, которые нельзя не учитывать при реализации параллельных процессов. И здесь у МКА и соответственно породившей ее МТ неоспоримые преимущества перед МП. Поэтому, когда знаешь недостатки и достоинства рассмотренных машин, можно сделать вывод о желательности и даже необходимости их «мирного» совместного существования. Так, в рамках действий и предикатов, к которым вполне применимо понятие «мгновенный», удобнее конструкция и модель машины Поста, а при реализации самих процессов, когда время нужно обязательно учитывать, — машина Тьюринга или МКА. Таким образом, можно говорить об архитектуре с иерархически вложенной структурой абстрактных машин.

Машина Тьюринга лучше

Итак, если мы хотим создать эффективную и универсальную параллельную модель и соответствующую ей архитектуру процессора, то должны взять за основу машину Тьюринга и тесно связанную с нею модель конечного автомата. В целом мы ее рассмотрели, а в каких-то деталях ее можно совершенствовать и даже можно «оттачивать» ее теорию, но общий подход остается прежним: параллельная модель — это множество машин Тьюринга, работающих в едином дискретном времени с синхронизацией с помощью внутренних состояний. Выше — модель СМКА на уровне множества параллельных процессов и модель МКА на уровне отдельных процессов (здесь, вероятно, даже лучше иметь комбинацию МКА и МП).

Все изложенное представляет собой не чисто теоретические построения, как это может показаться из-за оперирования абстрактными понятиями, а формализацию результатов продолжительной практической работы. Параллельная модель, определяющая конечно-автоматную модель программ, а в итоге и конечно-автоматную технологию программирования, работает достаточно давно и успешно. Данная технология показала свою эффективность, гибкость, удобство и приспособляемость (в смысле реализации на различных языках и в разных операционных средах) при решении самых сложных задач, требующих описания множества параллельно работающих, взаимодействующих параллельных процессов.

На этом практические эксперименты над абстрактными машинами можно завершить, а далее приступить к рассмотрению основ теории параллельных процессов на базе рассмотренной выше модели СМКА, т. е. того, без чего любая параллельная модель — набор блоков (как набор цифр в «кассе» первоклассника). Но это будет темой уже следующего теоретического эксперимента.

Литература