Что такое шифрование?
Шифрование используется человечеством с того самого момента, как появилась первая секретная информация, т. е. такая, доступ к которой должен быть ограничен. Это было очень давно — так, один из самых известных методов шифрования носит имя Цезаря, который если и не сам его изобрел, то активно им пользовался (см. врезку «Система шифрования Цезаря»).
Криптография обеспечивает сокрытие смысла сообщения и раскрытие его расшифровкой с помощью специальных алгоритмов и ключей. Ключ понимается нами как конкретное секретное состояние параметров алгоритмов шифрования и дешифрования. Знание ключа дает возможность прочтения секретного сообщения. Впрочем, как вы увидите ниже, далеко не всегда незнание ключа гарантирует то, что сообщение не сможет прочесть посторонний человек.
Процесс вскрытия шифра без знания ключа называется криптоанализом. Время, необходимое для взлома шифра, определяется его криптостойкостью. Чем оно больше, тем «сильнее» алгоритм шифрования. Еще лучше, если изначально вообще нельзя выяснить, достижим ли результат взлома.
Основные современные методы шифрования
Среди разнообразнейших способов шифровании можно выделить следующие основные методы:
- Алгоритмы замены или подстановки - символы исходного текста заменяются на символы другого (или того же) алфавита в соответствии с заранее определенной схемой, которая и будет ключом данного шифра. Отдельно этот метод в современных криптосистемах практически не используется из-за чрезвычайно низкой криптостойкости.
- Алгоритмы перестановки - символы оригинального текста меняются местами по определенному принципу, являющемуся секретным ключом. Алгоритм перестановки сам по себе обладает низкой криптостойкостью, но входит в качестве элемента в очень многие современные криптосистемы.
- Алгоритмы гаммирования - символы исходного текста складываются с символами некой случайной последовательности. Самым распространенным примером считается шифрование файлов "имя пользователя.pwl", в которых операционная система Microsoft Windows 95 хранит пароли к сетевым ресурсам данного пользователя (пароли на вход в NT-серверы, пароли для DialUp-доступа в Интернет и т.д.).
Когда пользователь вводит свой пароль при входе в Windows 95, из него по алгоритму шифрования RC4 генерируется гамма (всегда одна и та же), применяемая для шифрования сетевых паролей. Простота подбора пароля обусловливается в данном случае тем, что Windows всегда предпочитает одну и ту же гамму.
- Алгоритмы, основанные на сложных математических преобразованиях исходного текста по некоторой формуле. Многие из них используют нерешенные математические задачи. Например, широко используемый в Интернете алгоритм шифрования RSA основан на свойствах простых чисел.
Симметричные и асимметричные криптосистемы
Прежде чем перейти к отдельным алгоритмам, рассмотрим вкратце концепцию симметричных и асимметричных криптосистем. Сгенерировать секретный ключ и зашифровать им сообщение — это еще полдела. А вот как переслать такой ключ тому, кто должен с его помощью расшифровать исходное сообщение? Передача шифрующего ключа считается одной из основных проблем криптографии.
Оставаясь в рамках симметричной системы (так она названа оттого, что для шифрования и дешифрования подходит один и тот же ключ), необходимо иметь надежный канал связи для передачи секретного ключа. Но такой канал не всегда бывает доступен, и потому американские математики Диффи, Хеллман и Меркле разработали в 1976 г. концепцию открытого ключа и асимметричного шифрования. В таких криптосистемах общедоступным является только ключ для процесса шифрования, а процедура дешифрования известна лишь обладателю секретного ключа.
Например, когда я хочу, чтобы мне выслали сообщение, то генерирую открытый и секретный ключи. Открытый посылаю вам, вы шифруете им сообщение и отправляете мне. Дешифровать сообщение могу только я, так как секретный ключ я никому не передавал. Конечно, оба ключа связаны особым образом (в каждой криптосистеме по-разному), и распространение открытого ключа не разрушает криптостойкость системы.
В асимметричных системах должно удовлетворяться следующее требование: нет такого алгоритма (или он пока неизвестен), который бы из криптотекста и открытого ключа выводил исходный текст. Пример такой системы — широко известная криптосистема RSA.
Алгоритм RSA
Алгоритм RSA (по первым буквам фамилий его создателей Rivest-Shamir-Adleman) основан на свойствах простых чисел (причем очень больших). Простыми называются такие числа, которые не имеют делителей, кроме самих себя и единицы. А взаимно простыми называются числа, не имеющие общих делителей, кроме 1.
Для начала выберем два очень больших простых числа (большие исходные числа нужны для построения больших криптостойких ключей. Например, Unix-программа ssh-keygen по умолчанию генерирует ключи длиной 1024 бита).
Определим параметр n как результат перемножения p и q. Выберем большое случайное число и назовем его d, причем оно должно быть взаимно простым с результатом умножения (p -1)*(q -1).
Отыщем такое число e, для которого верно соотношение
(e*d) mod ((p -1)*(q -1)) = 1
(mod — остаток от деления, т. е. если e, умноженное на d, поделить на ((p -1)*(q -1)), то в остатке получим 1).
Открытым ключом является пара чисел e и n, а закрытым — d и n.
При шифровании исходный текст рассматривается как числовой ряд, и над каждым его числом мы совершаем операцию
C(i)= (M(i)e) mod n.
В результате получается последовательность C(i), которая и составит криптотекст. Декодирование информации происходит по формуле
M(i) = (C(i)d) mod n.
Как видите, расшифровка предполагает знание секретного ключа.
Давайте попробуем на маленьких числах.
Установим p=3, q=7. Тогда n=p*q=21. Выбираем d как 5. Из формулы (e*5) mod 12=1 вычисляем e=17. Открытый ключ 17, 21, секретный — 5, 21.
Зашифруем последовательность «12345»:
C(1)= 117 mod 21= 1
C(2)= 217 mod 21 =11
C(3)= 317 mod 21= 12
C(4)= 417 mod 21= 16
C(5)= 517 mod 21= 17
Криптотекст — 1 11 12 16 17.
Проверим расшифровкой:
M(1)= 15 mod 21= 1
M(2)= 115 mod 21= 2
M(3)= 125 mod 21= 3
M(4)= 165 mod 21= 4
M(5)= 175 mod 21= 5
Как видим, результат совпал.
Криптосистема RSA широко применяется в Интернете. Когда вы подсоединяетесь к защищенному серверу по протоколу SSL, устанавливаете на свой ПК сертификат WebMoney либо подключаетесь к удаленному серверу с помощью Open SSH или SecureShell, то все эти программы применяют шифрование открытым ключом с использованием идей алгоритма RSA. Действительно ли эта система так надежна?
Конкурсы по взлому RSA
С момента своего создания RSA постоянно подвергалась атакам типа Brute-force attack (атака методом грубой силы, т. е. перебором). В 1978 г. авторы алгоритма опубликовали статью, где привели строку, зашифрованную только что изобретенным ими методом. Первому, кто расшифрует сообщение, было назначено вознаграждение в размере 100 долл., но для этого требовалось разложить на два сомножителя 129-значное число. Это был первый конкурс на взлом RSA. Задачу решили только через 17 лет после публикации статьи.
Криптостойкость RSA основывается на том предположении, что исключительно трудно, если вообще реально, определить закрытый ключ из открытого. Для этого требовалось решить задачу о существовании делителей огромного целого числа. До сих пор ее аналитическими методами никто не решил, и алгоритм RSA можно взломать лишь путем полного перебора. Строго говоря, утверждение, что задача разложения на множители сложна и что взлом системы RSA труден, также не доказано.
Компания RSA (http://www.rsa.ru) регулярно проводит конкурсы на взлом собственных (и не только собственных) шифров. Предыдущие конкурсы выиграла организация Distributed.net (http://www.distributed.net/), являющаяся Интернет-сообществом добровольцев. Участники Distributed.net загружают к себе на ПК небольшую программу-клиент, которая подсоединяется к центральному серверу и получает кусочек данных для вычислений. Затем все данные загружаются на центральный сервер, и клиент получает следующий блок исходной информации. И так происходит до тех пор, пока все комбинации не будут перебраны. Пользователи, участники системы, объединяются в команды, а на сайте ведется рейтинг как команд, так и стран.
Например, участвующей в конкурсе по взлому RC5-64 (блочный шифр компании RSA, использующий ключ длиной 64 бита) организации Distributed.net удалось осуществить взлом через пять лет (1757 дней) работы. За это время в проекте участвовали 327 856 пользователей и было перебрано 15 268 315 356 922 380 288 вариантов ключа. Выяснилось, что была (не без юмора) зашифрована фраза «some things are better left unread» («некоторые вещи лучше оставлять непрочтенными»). Общие рекомендации по шифру RC5-64 таковы: алгоритм достаточно стоек для повседневных нужд, но шифровать им данные, остающиеся секретными на протяжении более пяти лет, не рекомендуется».
Сейчас организация Distributed.net взламывает шифр RC5-72 (ключ 72 бита длиной). Что интересно, добавление всего 8 бит в длину ключа привело к тому, что за 172 дня существования очередного конкурса по взлому было перебрано всего лишь 0,023% от всех ключей. Что ж, подождем...
Шифрование в Windows
Большинство из нас постоянно используют шифрование, хотя и не всегда знают об этом. Если у вас установлена операционная система Microsoft, то знайте, что Windows хранит о вас (как минимум) следующую секретную информацию:
- пароли для доступа к сетевым ресурсам (домен, принтер, машины в сети и т.д.);
- пароли для доступа в Интернет с помощью DialUp;
- кэш паролей (в браузере есть такая функция - кэшировать пароли, и Windows сохраняет все когда-либо вводимые вами в Интернете пароли);
- сертификаты для доступа к сетевым ресурсам и зашифрованным данным на самой машине.
Эти данные хранятся либо в pwl-файле (в Windows 95), либо в SAM-файле (в Windows NT/2000/ XP). Это файл Реестра Windows, и потому операционная система никому не даст к нему доступа даже на чтение. Злоумышленник может скопировать такие файлы, только загрузившись в другую ОС или с дискеты. Утилит для их взлома достаточно много, самые современные из них способны подобрать ключ за несколько часов.
Это является одной из причин, по которым в любой курс по обеспечению безопасности предприятия введены лекции о неинформационных средствах, а именно об охране, пропускном режиме, ограничении доступа посторонних лиц к компьютерам и т. д. Например, ограничения NTFS (файловая система Windows NT/2000) на доступ к данным не действуют в другой ОС. Если же злоумышленник сможет загрузить c дискеты MS-DOS, то любая информация из разделов NTFS может быть считана при наличии соответствующего драйвера, а такие драйверы уже существуют и для MS-DOS, и для Unix.
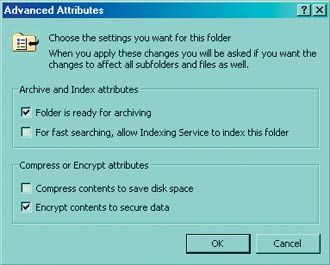
В операционную систему Windows 2000 встроена система шифрования EFS (Encrypting File System), позволяющая хранить некоторые блоки файловой системы NTFS в зашифрованном виде. Эта технология очень удобна, потому что работает как встроенный системный сервис. Для того чтобы зашифровать файл или каталог, нажмите на кнопку Advanced в свойствах файла или директории. В появившемся окне (рис. 1) отметьте галочкой Encrypt contents to secure data.
|
| Рис. 1 |
Когда Windows спросит, применять ли установленные параметры на поддиректории и входящие файлы, ответьте «Да». При шифровании каталога EFS гарантирует, что все файлы в нем будут зашифрованы. При этом вы продолжаете работать с этими директориями так же, как и раньше. Вам вовсе не обязательно производить дешифрацию файлов, чтобы открыть их — все происходит на системном уровне прозрачно и для пользователя, и для приложений.
Программы-шифраторы
Иногда необходимо зашифровать отдельный файл, чтобы передать его кому-нибудь или послать по электронной почте и т.д. Иногда нужно просто зашифровать файл, а стандартных возможностей, предоставляемых файловой системой NTFS, недостаточно. В таких случаях можно прибегнуть к помощи специальных шифрующих программ.
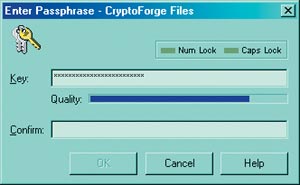
Например, CryptoForge (http://www.cryptoforge.com/) позволяет зашифровать файл любым из четырех алгоритмов (Blowfish, TripleDES, Gost и даже Rijndael — см. врезку «Конкурс AES»). Встраиваясь в систему, программа добавляет в контекстное меню проводника Explorer пункт Encrypt. Нажав на него, вы получите предложение ввести пароль (рис. 2).
|
| Рис. 2 |
Введенный пароль, который затем преобразуется в ключ, будет использован в качестве параметра для указанного в настройках алгоритма. Прочитать этот файл не сможет никто, кроме знающих пароль.
Цифровая подпись
Цифровая подпись — одно из самых распространенных применений шифрования. Суть цифровой подписи состоит в том, чтобы идентифицировать сообщение и гарантировать его неизменность. Сообщение (любой длины) преобразуется с помощью так называемой хэш-функции в короткое число. Обычно оно имеет размерность 128 бит. Хэш-функция однонаправлена (по числу нельзя восстановить сообщение) и однозначна (при повторном хэшировании того же сообщения получится то же число).
Теоретически существует множество сообщений, которые будут хэшированы в то же число, но на практике вероятность такого события ничтожно мала (см. врезку «Криптографические хэш-функции»).
Полученное в результате обработки хэш-функцией текста сообщения число шифруется по RSA-алгоритму на закрытом ключе пользователя и посылается адресату вместе с письмом и экземпляром открытого ключа. Адресат с помощью открытого ключа отправителя выполняет ту же хэш-функцию над пришедшим сообщением. Если оба числа равны, это означает, что сообщение подлинное, а если был изменен хотя бы один символ, то числа не совпадут.
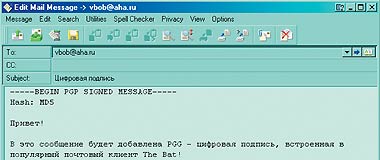
Один из самых распространенных в России почтовых клиентов, программа The Bat!, обладает встроенными возможностями добавлять цифровые подписи к письмам (обратите внимание на пункт меню Privacy при редактировании письма). Подробнее об этой методике читайте в статье «Электронная цифровая подпись» (см. «Мир ПК», № 3/02).
|
| Рис. 3 |
Криптография
Криптография — наука о принципах, средствах и методах преобразования информации для защиты ее от несанкционированного доступа и искажения. В последнее время она развивается очень и очень бурно. Это бесконечная увлекательная гонка, требующая много времени и сил: криптоаналитики взламывают алгоритмы, которые еще недавно были стандартами и повсеместно использовались. Кстати, недавно математики Дэн Голдстон (США) и Кем Илдирим (Турция) доказали первую закономерность в распределении простых чисел (до сих пор таких закономерностей не замечали). Простые числа располагаются на числовой оси некоторыми скоплениями, что несколько облегчает их поиск.
Математические исследования, ведущиеся во всем мире, постоянно приводят все к новым и новым открытиям. Как знать, может быть, мы стоим на пороге взлома алгоритма RSA или других криптосистем, основанных на нерешенных математических задачах.
Об авторе
Олег Бунин — специалист по разработке ПО для крупных Интернет-проектов, сотрудник компании «Рамблер», vbob@aha.ru.
Литература
- Лукашов И. В. Криптография? Железно! // Мир ПК. 2003. № 3 (http://www.osp.ru/pcworld/2003/03/100.htm).
- Панасенко С. П., Ракитин В.В. Аппаратные шифраторы // Мир ПК. 2002. № 8 (http://www.osp.ru/pcworld/2002/08/077.htm).
- Панасенко С. П. Чтобы понять язык криптографов // Мир ПК. 2002. № 5 (http://www.osp.ru/pcworld/2002/05/086.htm).
- Панасенко С. П. Чтобы понять язык криптографов // Мир ПК. 2002. № 6 (http://www.osp.ru/pcworld/2002/06/091.htm).
- Панасенко С. П. Электронная цифровая подпись // Мир ПК. 2002. № 3 (http://www.osp.ru/pcworld/2002/03/078.htm).
- Панасенко С. П. Защита информации в компьютерных сетях: шифрование // Мир ПК. 2002. № 2 (http://www.osp.ru/pcworld/2002/02/070.htm).
- Дмитриев А. Системы защиты информации // Мир ПК. 2001. № 5 (http://www.osp.ru/pcworld/2001/05/010.htm).
- Введение в криптографию / Под ред. В.В. Ященко. М.: МЦНМО, 2000.
- Носов В. А. Краткий исторический очерк развития криптографии // Материалы конференции "Московский университет и развитие криптографии в России", МГУ, 17-18 октября 2002 г.
- Саломаа А. Криптография с открытым ключом. М., 1996 .
- Циммерман Ф. PGP - кодирование с открытым ключом для всех.
Система шифрования Цезаря
Пример алгоритма замены — система шифрования Цезаря. Этот метод основан на замене каждой буквы сообщения на другую путем смещения от исходной на фиксированное количество символов. Попробуйте расшифровать четверостишие Омара Хайяма (время выполнения — 10 минут).
РЛЗЬ ЁМЭЙЗ АВБЖУ ИЙЗАВЛУ, БЖЩЛУ ЖЩЭЗЬЖЗ ЖЮЁЩЕЗ, ЭЫЩ ЫЩАЖФО ИЙЩЫВЕЩ БЩИЗЁЖВ ЭЕШ ЖЩРЩЕЩ: ЛФ ЕМРСЮ ЪЗЕЗЭЩГ, РЮЁ РЛЗ ИЗИЩЕЗ ЮКЛУ, В ЕМРСЮ ЬМЭУ ЗЭВЖ, РЮЁ ЫЁЮКЛЮ К ДЮЁ ИЗИЩЕЗ.
Успели? Привожу «отгадку»:
Чтоб мудро жизнь прожить, знать надобно немало,
Два важных правила запомни для начала:
Ты лучше голодай, чем что попало есть,
И лучше будь один, чем вместе с кем попало.
Ключ для расшифровки: сдвигаем на семь символов (берем седьмой) влево по алфавиту. Алфавит закольцован. Регистр символов не учитывается.
Windows и пароли
Как Windows шифрует пароли?
Система берет пароль, преобразует его в верхний регистр, обрезает до 14 символов, затем делит их на две половины по 7, шифрует каждую по отдельности и так сохраняет, что несколько упрощает взлом. Кстати, когда будете придумывать пароль, имейте в виду, что комбинация длиннее 14 символов имеет мало смысла.
Конкурс AES (Advanced Encryption Standard)
В 80-х гг. в США приняли стандарт симметричного шифрования для внутреннего применения — DES ((Data Encryption Standard, подобный стандарт есть и в России). Но в 1997 г., когда стало понятно, что 56-битового ключа DES недостаточно для надежной криптосистемы, Американский институт стандартизации объявил конкурс на новый стандартный алгоритм. Из 15 вариантов был выбран лучший: бельгийский алгоритм Rijndael (его название составлено из фамилий авторов — Rijmen и Daemen, читается как «Рэйндал». Этот алгоритм уже встроен в различные криптографические средства, поставляемые на рынок). Другими финалистами конкурса стали MARS, RC6, Serpent, TwoFish. Все эти алгоритмы были признаны достаточно стойкими и успешно противостоящими всем широко известным методам криптоанализа.
Криптографические хэш-функции
Криптографические хэш-функции преобразуют входные данные любого размера в строку фиксированного размера. Для них чрезвычайно сложно найти:
- два разных набора данных с одинаковым результатом преобразования (стойкость к коллизиям); например, количество арифметических операций, необходимых для того, чтобы найти блок данных, также имеющий краткое сообщение для хэш-функции MD5, составляет приблизительно 2 64;
- входное значение по известному результату хэширования (необратимость); для MD5 предполагаемое количество операций, необходимых для вычисления исходного сообщения, равно 2 128.
