Сегодня мы разберем задачу «Эчпочмаки»¹, написанную мной для подготовки учеников к олимпиадам.
Условие
С приближением холодов любимая крыса Василия Федоровича собралась готовить запасы на зиму. К ее радости, хозяин неожиданно решил продемонстрировать свое кулинарное мастерство и приготовил N эчпочмаков, которые по забывчивости оставил без присмотра.
В системе жизненных ценностей крысы эчпочмаки определяются как треугольники, заданные длинами своих сторон, правда, из-за отсутствия мастерства у кулинара эчпочмаки получались в виде произвольных невырожденных треугольников. Основное качество эчпочмака, по логике крысы, — это площадь: чем она больше, тем «пропитание» ценнее.
Крыса была бы рада утащить себе в нору, прогрызенную в полости дивана, самый ценный эчпочмак целиком, но щель имеет ограниченные размеры и не все пирожки могут туда пролезть. Ширина этой щели равна D (вещественное число) и измеряется в сантиметрах. В плоскости отверстия эчпочмак может быть ориентирован произвольно, и если хотя бы в одном из положений он проходит в щель, то считается подходящим.
Необходимо найти номер наиболее ценного эчпочмака, который проходит в отверстие.
Входные данные
Во входном файле записаны целое число N (количество эчпочмаков; 1 Пример входного файла a.in
В выходной файл выведите номер наиболее ценного эчпочмака, пролезающего в щель. Если существует несколько различных правильных ответов, то выведите любой из них. Если же ни один из эчпочмаков протащить невозможно, выведите 0. Пример выходного файла a.out
Комментарий к примеру На рис. 1 представлен эчпочмак 1, проходящий в щель, если он определенным образом сориентирован, а эчпочмак 2 не поместится туда ни при каких условиях. Введем ось X, направленную перпендикулярно прямой, содержащей отверстие. Произвольно сориентируем треугольник в плоскости и начнем двигать его вдоль оси X (рис. 2). Введем функцию d(x), значение которой равно длине отрезка, лежащего в треугольнике на прямой, содержащей отверстие. Несложно доказать, что с момента прохода вершины A и до момента достижения вершины B функция d(x) будет возрастающей, а затем, до вершины C, — убывающей (при доказательстве можно воспользоваться подобием треугольников). Следовательно максимума функция d(x) достигнет тогда, когда точка B (средняя вершина треугольника) будет лежать на прямой. Значит, чтобы узнать, пройдет ли треугольник сквозь отверстие, достаточно посчитать значение функции d(x) в средней вершине и выяснить, не больше ли оно, чем размеры отверстия. Определим наилучшую ориентацию треугольника. Один конец отрезка, задающего пересечение прямой и треугольника, — его средняя вершина, второй лежит на противоположной стороне. Кратчайшее расстояние от вершины треугольника до его противоположной стороны — высота. Понятно, что треугольник надо ориентировать так, чтобы его наименьшая высота была параллельна прямой, содержащей отверстие. Вычислить площадь треугольника можно по формуле Герона: S = sqrt (p.(p-a).(p-b).(p-c)), где a, b, c — длины сторон треугольника; p — полупериметр. Длину наименьшей высоты h можно вычислить, пользуясь формулой для площади треугольника S = 1/2.h.a, где a — наибольшая сторона. Значит, h = 2.S/a. Для решения задачи просто перебираем все треугольники и запоминаем номер того, у которого наибольшая площадь и минимальная высота не больше размеров отверстия. ¹Эчпочмак — татарское национальное блюдо, пирожок с мясом и картофелем. Слово «эчпочмак» переводится с татарского как «треугольник». Листинги с решением этой задачи, а также тестовые входные и выходные файлы для проверки вашего решения помещены на «Мир ПК-диске».
2 10
10 10 10
20 17 20Выходные данные
1

Рис. 1. Такие вот получились эчпочмаки
Решение
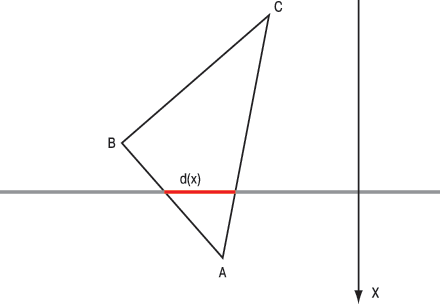
Рис. 2. Так пирожок должен проходить в щель
