Цветное программирование

Естественным объектом восприятия и переработки информации, присущим человеку от природы, является цветовой образ. Не открытие, что цветные графика и текст в отличие от черно-белой графической и текстовой информации придают новое качество полученному образу. Наряду с цветной электронной и печатной графикой цветная палитра для текста уже достаточно давно применяется, например, для обозначения ссылок в гипертекстовых и веб-документах.

Черная точка на белом фоне позволяет отобразить лишь 1 бит, а цветная на современном мониторе — до 32 бит (232 цветовых оттенка) формально, но до 4—5 бит (16—32 явно различимых цветовых оттенка), дискретно воспринимаемых человеком. Поэтому отрезок черной линии на белом фоне несет лишь единственный смысл (наличие связи между двумя объектами, отождествляемыми с концами отрезка, если не учитывать кривизну линии, характеризующую промежуточную среду). Однако если такой же отрезок, хотя бы монохромно окрасить каким-либо цветом из заданной цветовой палитры, то он будет иметь уже множественный смысл (отражая не только наличие связи между объектами, но и ее качественный характер, например, 16 градаций при использовании 16-цветной палитры, кодируемой 4 битами). В то же время если два или более участка того же отрезка окрашены в разные цвета, то кодируются и передаются уже 1+16^N смысловых оттенков.

Черно-белая палитра текстовых документов негативно влияла как на преимущественное развитие математической двоичной логики (в отличие от многозначной и непрерывной — аналоговой), так, на наш взгляд, и на до сих пор применяемую концепцию цифровой, сугубо бинарной вычислительной техники. Это отразилось и на системах команд вычислительных машин (только двоичный выбор в команде условного перехода) и на управляющих структурах алгоритмов и программ (непременное бинарное условие ЕСЛИ—ТО—ИНАЧЕ почти во всех алгоритмических языках). В таком бинарном программировании рассматриваются всего два варианта ветвления по типу «да» — «нет» («выполнено» — «не выполнено»), в то время как в реальной жизни и в реальных управляемых программами объектах различной природы вариантов исхода при проверке условий всегда больше двух. В некоторые алгоритмические языки включены операторы как множественного выбора, так и обработки исключительных ситуаций.

Новые, предлагаемые в данной статье возможности представления алгоритмов и программ с использованием цветовой палитры обеспечивают компактность представления, усиливают его информационную емкость, упрощают процессы алгоритмизации, кодирования, восприятия и понимания алгоритмов и программ, позволяют обучать логическому мышлению в раннем детском возрасте, дают возможность объективного суждения об индивидуальности программиста, расширяют горизонты шифрования.

Сравнение простой бинарной функции

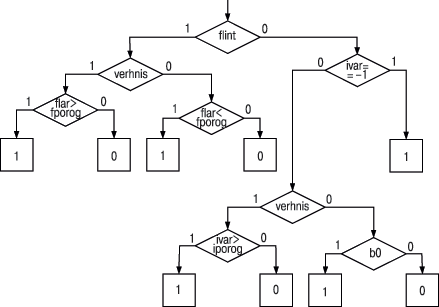
Для представления алгоритмов, независимых от используемого языка программирования, в основном применяются граф-схемы [1] (блок-схемы) и диаграммы (графы) переходов [2]. На рис. 1 представлена в виде общеупотребительной граф-схемы простая бинарная функция, определяющая факт выхода некоторого контролируемого параметра за пределы заданной пороговой величины (значения параметра и порога бывают как действительными, так и целыми числами; выход возможен в сторону как увеличения, так и уменьшения значения относительно порога). Функция возвращает двоичное значение: 1 — параметр выходит за заданный предел, 0 — параметр в норме. При этом использованы черные линии и текст на белом фоне, а изображение граф-схемы в программной документации занимает одну страницу формата А4.

Рис. 1. Граф-схема бинарной функции

Размещение цветов базовой палитры образует радугу: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый (рис. 2). Для этих семи основных цветов можно употреблять белый или черный (либо оттенки серого) фон.

Рис. 2. Базовая палитра

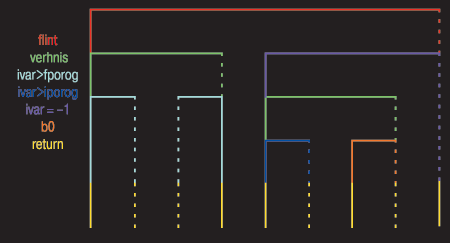
Воспользуемся ранее широко применявшимся (в MS DOS) черным фоном и отобразим на нем указанной цветовой палитрой один из вариантов рассмотренной граф-схемы бинарной функции (рис. 3). В левой части рис. 3 перечислены текстовые логические условия, принятые в бинарных операторах (в ромбах) на рис. 1, но окрашенные цветами палитры (см. рис. 2). В правой части рис. 3 предлагается цветовое решение отображаемой граф-схемы. Каждая горизонтальная линия обозначает логическое условие, цвет которого совпадает с цветом текста условия в левой части рис. 3. Вертикальные линии представляют собой соответствующее ветвление: сплошная линия - единичное значение (выполнение) логического условия; пунктирная - нулевое значение (невыполнение) того же условия. Таким образом, бинарному оператору выбора соответствуют три линии одного цвета: сплошная горизонтальная и примыкающие к ней вертикальные - сплошная и пунктирная. Исключением являются желтые вертикальные линии (сплошная - 1 и пунктирная - 0), обозначающие возвращаемое функцией значение.

Рис. 3. Цветовая схема бинарной функции

Сравнение рис. 1 и 3 позволяет сделать вывод, что второй гораздо компактнее первого. Повторяемость логических условий, а также назначение единичных и нулевых ветвей выполнения логических условий воспринимается практически мгновенно. Структурная сложность рис. 3, т.е. общее количество возможных маршрутов в схеме алгоритма [3], оценивается существенно быстрее и легче, чем для рис. 1. Причем проявляется совершенно новое качество такой оценки цветовой схемы — резкое снижение трудоемкости анализа алгоритма (это требует отдельного рассмотрения). Впрочем, есть и другие положительные черты представленного на рис. 3 варианта цветового решения отображения граф-схемы.

Цветные схемы алгоритмов

Имеется множество различных вариантов отображения цветных схем алгоритмов (ЦСА). Например, можно не по отдельности обозначать цветом текстовые логические условия, а размещать их поверх горизонтальных цветных отрезков. Это, с одной стороны, несколько увеличит площадь самой схемы, с другой — уменьшит общую площадь изображения. Можно также каждое логическое условие вместе с подробным комментарием выделить в текстовой части документа с обязательной цветовой пометкой, например, в следующем виде:

- flint — параметр с плавающей запятой (1) или целочисленный (0).

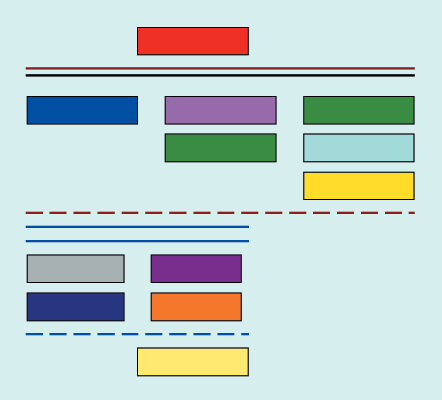
Здесь отрезок прямой показан выбранным цветом, используемым далее на рис. 4.

Рис. 4. Параллельно-последовательная схема

Поскольку любой сложный алгоритм можно представить в виде параллельно-последовательной схемы (ППС) независимых и зависимых фрагментов [4], то допускается использовать цветные ППС и детализировать отдельные фрагменты ППС в виде соответствующих ЦСА, подобных рассмотренному на рис. 1, 3 примеру.

Распараллеливание ветвей в ППС можно отображать горизонтальными двойными линиями одного цвета, а сборку параллельных ветвей — горизонтальным пунктиром того же цвета (рис. 4). Подразумевается, что последовательность зависимых фрагментов всегда идет сверху вниз, поэтому вертикальные связующие линии необязательно и указывать.

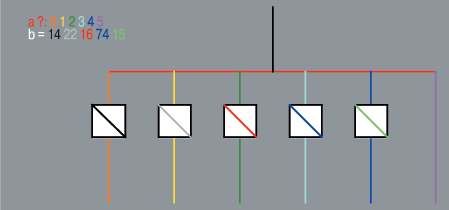
Особое внимание следует уделить множественному выбору. В случае бинарных алгоритмов (см. рис. 3) достаточно кодировать единичную и нулевую ветви тем же цветом, что и бинарное условие. В случае множественного ветвления допускается для каждой ветви (вертикальной линии) установить свой цвет, а не давать их пунктиром, и объяснить эти цвета в текстовой части рисунка алгоритма (рис. 5) или непосредственно привести текст поверх линий.

Рис. 5. Множественный выбор

Линейные операторы типа присваивания и вызова функций можно указывать цветным прямоугольником. Так, если присваивание выполняется для одной и той же переменной по нескольку раз, то все соответствующие прямоугольники, закрашенные цветом, выбранным для такой переменной, дополнительно помечаются, например, линией, характеризующей каждый новый вариант присваивания (см. рис. 5). Вариантов подобных пометок достаточно много.

Что же следует предпринять при нехватке набора цветов палитры? Один из вариантов — использовать двойные линии разного цвета или на одной линии выделять разноокрашенные отрезки.

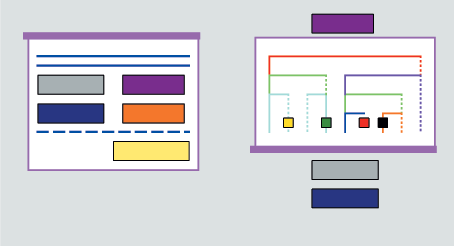
В схемах алгоритмов существует два основных вида циклических конструкций: условие перед входом в цикл и условие перед выходом из цикла. Циклы в ЦСА предлагается выражать прямоугольной рамкой, окрашенной в выбранной для условия цикла цвет со значительно утолщенной верхней или нижней линией, обозначающей проверку условия перед входом в цикл или перед выходом из него соответственно. На рис. 6 изображены две циклические ППС: одна — с проверкой условия перед входом в цикл, другая — перед выходом из него (текстовая часть для упрощения опущена).

Рис. 6. Циклические схемы

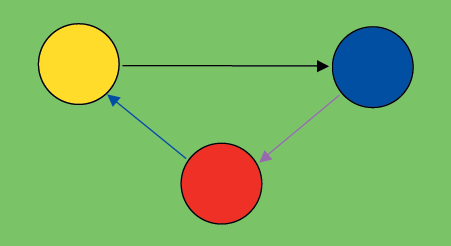
Аналогично и диаграммы (графы) переходов конечных автоматов окрашиваются как в части дуг переходов (цвет дуги маркирует входную букву автомата, а дополнительная пометка на дуге типа цветного прямоугольника кодирует букву выходного алфавита Мили), так и в части вершин — состояний автомата, цвет которых кодирует букву выходного алфавита Мура. При этом под буквами входного и выходного алфавитов подразумеваются сложные логические выражения и операции присваивания и вызовы функций соответственно. Простейший пример графа переходов, не нагруженный текстовой информацией, представлен на рис. 7.

Рис. 7. Граф переходов

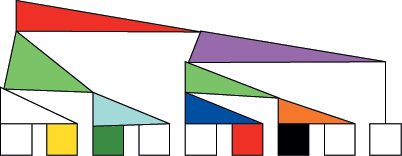
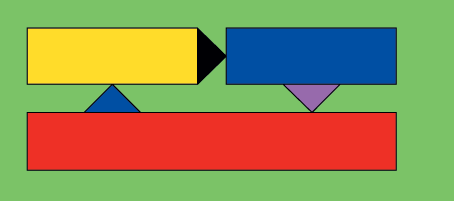
Каждый программист в состоянии предложить не один вариант цветокодирования ЦСА, в том числе и такие, которые несколько удалены от стандартного представления. На рис. 8 и 9 приведены примеры, отображающие фрагмент рис. 6 и полностью рис. 7 соответственно, а также совершенно новые графические цветовые решения.

Рис. 8. Блок решений

Рис. 9. Граф переходов

Цветовое кодирование данных, выражений, функций и объектов классов

Обобщая типы переменных, принятых в большинстве алгоритмических языков, выделим следующие:

• целочисленные (булевы, байтовые, 2-, 4- и 8-байтовые)
• дробные (2-, 4- и 8-байтовые)
• строковые (неограниченного размера).

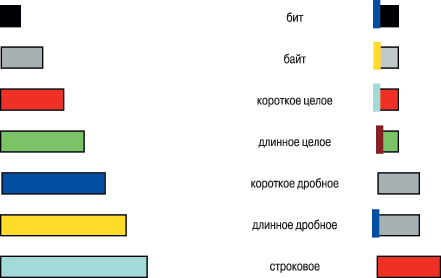
В случае цветового кодирования можно в принципе отказаться от символьных аббревиатур переменных и использовать только цветные элементарные геометрические фигуры для обозначения переменных как в алгоритмах, так и в программах. Для переменных указанных групп, к примеру, можно выбрать прямоугольники, одинаковые по высоте, но дискретно различимые по горизонтали в зависимости от типа. Или можно взять другой вариант, где переменные указанных трех групп имеют три размера, типы внутри которых различимы вертикальной цветной полосой на общем фоне цветного обозначения переменной (рис. 10).

Рис. 10. Переменные различных типов

Каждая переменная может быть выделена несколькими цветами, характеризующими тип, группу, подгруппу и т.д. Переменная типа «структура» обозначается несколькими уровнями, причем возможно как горизонтальное, так и вертикальное размещение групп переменных и субструктур.

Массивы дополнительно кодируются указателем мерности и размеров также с помощью цветных обозначений констант. Цифровые значения этих констант желательно не употреблять, поскольку они могут изменяться в процессе проектирования и в режиме исполнения программы. Так, трехмерный массив обозначается размещенными рядом тремя цветными прямоугольниками, соответствующими целым числам и ограниченными каким-либо специальным графическим примитивом, окрашенным в цвет, который обозначает массив переменной. Для выражений следует применять цветные иерархические геометрические постройки по типу каскадного представления операций при наглядном изображении сложного логического выражения (рис. 11).

Рис. 11. Отображение булева выражения вида (k=!a V b V !c)(d V e!f)(g V !h)

Функция с параметрами обозначается как горизонтальная последовательность цветных прямоугольников, соответствующих формальным (фактическим) параметрам, заключенным, например, между двумя разнонаправленными треугольными символами типа < и >. Цвет этих символов свидетельствует о конкретной функции. Между группой входных и группой выходных параметров желательно установить разделитель.

Класс в виде совокупности переменных и функций, закодированных цветом, сгруппированных соответствующим образом и размещенных, как сейчас принято, друг под другом, задается объемлющей рамкой или затушеванным прямоугольником, объемлющим переменные и функции. Цвет рамки или фона прямоугольника является идентификатором класса. Объекты данного класса и открытые его члены и методы должны включать в геометрическом цветном изображении обязательную цветовую компоненту, идентифицирующую этот класс.

Цветные тексты программ

Принятые в настоящее время раскраски листингов программ, получаемые в среде разработки типа Visual Studio, Borland C++ и др., не несут качественной нагрузки, рассмотренной выше. Если использовать средства цветового выделения текстовых структур в приведенном выше аспекте, то можно существенно сократить объемы листингов за счет уменьшения длины идентификаторов переменных и переноса их смысловой нагрузки на цвет идентификатора, а также за счет группирования обозначений их одинаковой (в том числе частичной) окраской. Это улучшит восприятие программ и упростит их анализ. Однако процесс подобного раскрашивания в системах разработки программ пока еще затруднен.

Выбрав цвет как основу языка программирования, можно создавать новые языки на основе существующих, но с упрощенным текстовым синтаксисом и с незначительным введением графических элементов. Например, оператор выбора (не следует в новом языке разделять бинарный и множественный выбор) представляется следующим образом. Слева указывается цветной идентификатор проверяемой переменной, справа от него проводится вертикальная линия того же цвета (на число строк, реализующих возможные варианты выбора). Правее этой вертикали в каждой строке указывается цветная константа, переменная или выражение, сопоставление с которыми на равенство (неравенство) дают искомые ветви выбора, а затем в каждой такой строке перечисляются операторы, соответствующие выбранной ветви. Нечто подобное можно предложить для реализации циклов и других языковых конструкций. При этом благодаря применению цвета и примитивных элементов графики удается вообще отказаться от отдельных ключевых слов типа if, while, for, switch, int, boolean, float и проч.

Для реализации чисто графического языка, наброски элементов которого представлены выше, требуется создание специализированной среды разработки, включающей графический редактор и конвертер в один из универсальных языков (С++, C#, Java). Но прежде требуется обсудить элементы такого языка, чтобы выработать один или несколько стандартов.

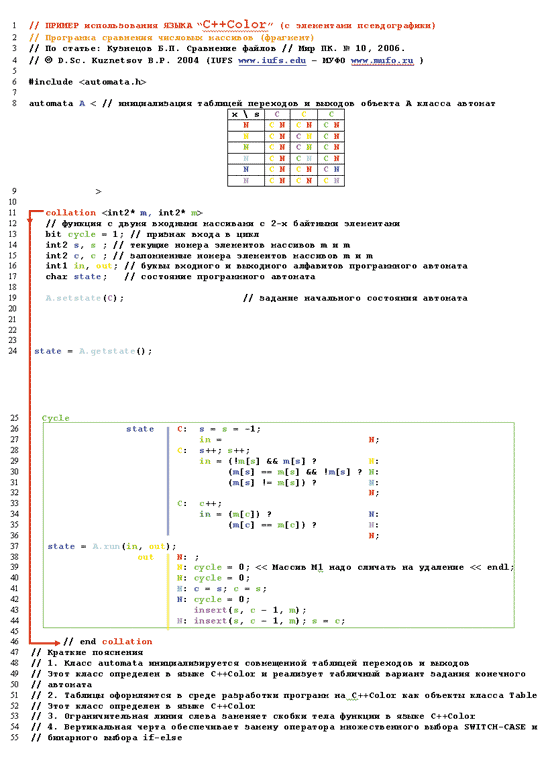
На рис. 12 приведен листинг с текстом программы на предполагаемом языке программирования С++Сolor.

Рис. 12. Текст программы на предполагаемом языке программирования С++Сolor.