Трехмерная графика своими руками. Часть 2. Follow the Ray

. В феврале («Мир ПК», №2/07, с. 60) мы только открыли его и боролись за простейшие, низкоуровневые операции, а также получили орудие, которым можно создавать и оттачивать формы. Нам стали доступны методы управления графическим процессором через библиотеку OpenGL. Модели объектов мы, словно искусным тесаком, вытачиваем из векторного пространства — задаем все больше и больше вершин, уточняя изгибы и линии.

Сделаем следующий шаг к реалистичности
Посмотрите вокруг. Мир словно гора сокровищ. Богатство его красок обусловлено не только разнообразием форм, но и красотой материалов. Зеркальные глади, сияющие блики, мягкие отсветы — не это ли позволяет миру иногда затрагивать ваши чувства? Посмотрим, как можно реализовать в графике такие, казалось бы, неуловимые эффекты.

Заглянем в физику явления
Солнечный луч, как и луч от любого другого источника света, падая на поверхность, поглощается, отражается и преломляется. В каких долях происходят эти явления — определяет материал поверхности. Что касается поглощения, то оно наблюдается, как правило, лишь в части спектра, из белого света поглощается только часть составляющих его цветов. Остаток светового потока, имеющий уже цветной оттенок, отражается от поверхности или частично проходит насквозь, если материал прозрачен. Таким образом порождаются два новых луча, каждый из которых начинает прямолинейное движение и, оказываясь в такой же ситуации при столкновении с препятствием, порождает в свою очередь новые лучи. В этом хитросплетении прямолинейно движущихся фотонов находится человеческий глаз, подвергаясь бомбардировке этими частицами и фиксируя интенсивность и цвет попадающего в него излучения. Так мы видим цветную картинку.
Идеология трассировки лучей (Ray Tracing) основана на этом же принципе. Представим некую сцену с объектами и источниками света, а также экран, через который смотрит наблюдатель. Задача заключается в том, чтобы построить правильное изображение на экране. С физической точки зрения логично было бы следить за лучом, испускаемым источником света, а также за всеми порожденными им при соударении потомками. Тогда часть лучей, которая попадет на экран, даст информацию об итоговой картине.
Проблема лишь в том, что в таком случае подавляющее большинство испускаемых лучей рассеется в пространстве, так и не достигнув экрана. Почти все вычисления окажутся бесплодными. Это ведет к немыслимым потерям производительности и делает такой алгоритм практически неприменимым.

Решение проблемы производительности
Трюк заключается в том, чтобы отслеживать ход лучей, обратный естественному, как бы испуская лучи из глаза наблюдателя. Решение обратной задачи полностью повторяет решение прямой, но эффективность и скорость выполнения обратной трассировки гораздо выше и достигает уже приемлемых результатов. Впервые в упрощенной форме этот алгоритм был предложен Артуром Аппелем в 1968 г. Он предложил выпускать луч из точки наблюдения через каждый пиксел экрана, а затем находить его ближайшее пересечение с объектами сцены. Схематично этот алгоритм выглядит так:

Для каждого пиксела экрана{
Выпустить луч из точки наблюдения через этот пиксел.
Инициализировать ближайшее расстояние Tnear = infinity, ближайший объект Onear = null.
Для каждого объекта Object в сцене{
Если луч пересекает этот объект{
Если расстояние t до пересечения меньше Tnear{
 Tnear = t,
 Onear = Object.
}
}
}
Вычислить цвет пиксела по материалу объекта Onear и его освещенность в точке пересечения с лучом.
}

Освещенность здесь рассчитывается классическими алгоритмами исходя из расположения объекта по отношению к источнику света. Этот прием графической визуализации использовался в исследованиях по радиоактивности и впоследствии применялся при разработке защиты от радиации.

Вход в рекурсию
В 1979 г. алгоритм был существенно развит и приобрел тот вид, в котором он известен под названием трассировки лучей. Тернер Уиттед предложил порождать из точки пересечения луча с поверхностью три новых луча так, как показано на рис. 1.

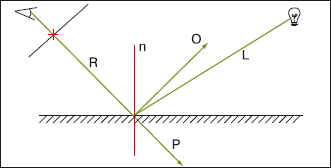
Здесь изображен начальный этап трассировки — из точки наблюдения через экран выпускается луч R. Процесс нацелен на определение цвета того пиксела экрана, который помечен красным крестом.
Луч R встречает на своем пути препятствие, частично проходит насквозь в виде луча P и частично отражается от поверхности под углом к нормали, равным углу падения, в виде луча O. Параметры материала определяют доли зеркального отражения и пропускания. Далее лучи O и P трассируются рекурсивно по тому же алгоритму, словно бы они были выпущены из точки наблюдения. Рекурсивная функция поставляет результат — цвет пиксела, затем этот цвет умножается на соответствующий коэффициент для каждого из двух лучей и суммируется в итоговом цвете для функции трассировки луча P. Луч L определяет первичную освещенность, их может быть несколько — по количеству источников света, их задача — определить количество света, попавшего в точку напрямую от источника. Если на пути L находится непрозрачный объект, то первичная освещенность считается равной нулю.
Трассировка потомков останавливается при достижении порогового числа уровней рекурсии. Например, отслеживается не более четырех поколений лучей. Можно также отсекать трассировку слишком темных лучей, вклад которых в итоговый цвет заведомо незначителен.

Что дает эта идея
Мы получаем почти идеальный расчет освещенности сцены. Мягкие переливы цветов, затененность, отражения, даже такой тонкий эффект, как цветные отсветы от яркого объекта на находящейся рядом светлой поверхности, точно и правильно прорисовываются на картине как естественное следствие алгоритма. Единственное, чего не учитывает описанная геометрическая модель, — это так называемое диффузное отражение, рассеяние, которое всегда возникает при столкновении луча с препятствием. Такое отражение происходит с равной интенсивностью во всех направлениях, поэтому для него нельзя указать вектор. Для компенсации этого эффекта вводится небольшое равномерное фоновое освещение. Во всем остальном модель безукоризненна с тем лишь исключением, что рендеринг сцены может занимать от нескольких минут до нескольких дней (или ночей), и это без учета анимации. Движущиеся ролики создаются так же, как классические мультфильмы, — прорисовывается каждый кадр, а затем они склеиваются, скажем, по 15 штук на секунду.

Реализация алгоритма
В терминах объектно-ориентированных языков типа С++ и С#, нужно создать класс Ray с полями, в которых хранятся начальная точка и направление луча, и метод Trace. Необходим класс Object с виртуальными методами vector3 Intersect и color DropRays и полем material, от этого класса будут наследоваться все объекты в сцене. Реализация Intersect для каждого объекта будет своей, но возвращать он должен координаты точки пересечения луча с объектом.
Необходимо создать коллекцию (или список) объектов типа Object и складировать в нее все имеющиеся в сцене объекты. Метод Ray.Trace должен принимать на вход указатель на коллекцию и последовательно выполнять Intersect для каждого объекта в списке. После нахождения ближайшего пересечения вызывается DropRays для объекта Onear — это функция, которая выбрасывает из найденной ранее точки пересечения три новых луча, как было описано выше, и запускает для каждого из них трассировку, получая от нее на выходе цвет пиксела. Затем DropRays суммирует эти цвета с весовыми коэффициентами, определяемыми материалом, и возвращает итоговый цвет пиксела. Это значение поступает в вызванный ранее метод Ray.Trace, для того чтобы быть выведенным на экран. Для закрашивания экрана можно использовать механизм OpenGL.
Алгоритм реализуется не очень сложно, так какие же остались проблемы? Какие задачи на самом деле предстоит решать?
Это задачи аналитической геометрии. Сложность алгоритма кроется в процессе отыскания точки пересечения луча с объектами сцены. Около 95% времени при обработке сложных сцен занимает именно эта операция. Чем сложнее объект, тем более запутанным может быть алгоритм, определяющий пересечение.

Пересечение со сферой
Нам предстоит узнать, что без математики и шага не сделать и что справочник по аналитической геометрии — настольная книга любого программиста, занимающегося трассировкой лучей.
Для отыскания точки пересечения луча с произвольной поверхностью необходимо знать аналитические уравнения, определяющие оба эти объекта в трехмерном пространстве. Точка пересечения удовлетворяет всем уравнениям, так как принадлежит и лучу, и поверхности. Поэтому, сводя уравнения в систему и находя ее решения, мы получаем координаты этой точки.
Найдем пересечение луча и сферы. Пусть из точки А выпущен луч в направлении вектора d, как показано на рис. 2.

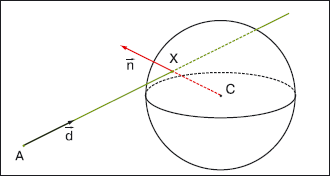
Уравнение луча: x = A + td, где t — неотрицательный параметр.
Ищем пересечение со сферой с центром в точке С радиуса r.

Ищем наименьшее неотрицательное значение t_min,
тогда точка пересечения имеет координаты x = A + t_mind.
|A + td – C|² = r²
Обозначим s = C – A, тогда
|td – s|² = (td – s, td – s) = t²d² – 2t (d,s) + s²,
где (d,s) — скалярное произведение векторов d
и s, равное сумме попарных произведений их коор-
динат.
Получаем квадратное уравнение на t:
d²t² – 2(d,s)t + s² = r²
Дискриминант D = 4. [(d,s)² – d²(s² – r²)].
Если D < 0, то луч проходит мимо сферы, если же D ≥ 0, то уравнение имеет действительные корни:
 
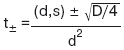
Наименьшее положительное значение t, если оно существует, дает ответ задачи. Если же положительного значения нет, то луч сферу не пересекает.
Если точка пересечения найдена, то нас будет интересовать также нормаль к поверхности в этой точке, так как эта нормаль определяет направление отраженного луча. В случае сферы все предельно просто — нормаль в точке имеет направление вектора, выпущенного из центра сферы в эту точку. В принятых обозначениях это X – C, учитывая нормировку по длине,
 

Пересечение с плоскостью
Предлагаю рассмотреть еще одну задачу, которую придется решать каждому, кто постигает трассировку лучей. Практически в любом проекте существует некая плоскость, будь то гладь морская или зеркальный стол. Давайте разберемся, как правильно ее визуализировать.
Плоскость задается общим уравнением: (x,n) = r, где n — вектор нормали с плоскости, имеющий единичную длину, а r — расстояние от начала координат до плоскости (с точностью до знака).
Решаем систему:
 
(A + td, n) = (a,n) + t (d,n) = r,
где а — вектор, имеющий координаты точки А. Тогда

Если (d,n) = 0, то луч параллелен плоскости, т.е. не пересекает ее.
Если же (d,n) ≠ 0, то вычисляем t. Тогда если его значение положительно, то луч пересекает плоскость. Координаты точки пересечения: X = A + t_xd.
Нормаль, которая будет использоваться при дальнейшем вычислении отраженного луча, должна составлять тупой угол с направляющим вектором d луча (рис. 3).

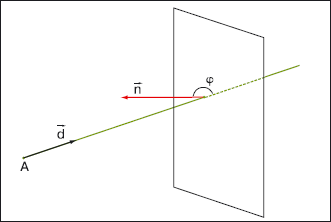
Если учесть, что
(d,n) = |d| |n| cosø,
где ø — угол между векторами d и n, то в качестве значения нормали нужно брать n (– sgn(d,n)).
Поздравляю! Вы справились с математической частью, поэтому теперь можно вернуться к лирике и поговорить об... оптимизации.

Методы оптимизации
Объекты реального мира можно с некоторой степенью точности аппроксимировать большим числом простых геометрических фигур. Если задуманное вами тело прозрачно, то не забывайте «удалять» грани, на которых эти простые фигуры склеиваются. Таким образом, вы получите огромное число процедур, каждая из которых должна будет выполниться для каждого луча и всех его потомков. Звучит устрашающе, и действительно, выполнение такой программы может затянуться на многие часы. Как можно улучшить ситуацию?
Начнем с того, что сложный объект, состоящий из большого числа фигур, можно поместить внутрь сферы. Тогда если луч не пересекает сферу, то он не пересечет и сам объект. На этом простом соображении построены более сложные методы:

1. Группа объектов заключается внутрь сферы. Проверяется, пересекает ли луч сферу. Если пересечения нет, то группа выбрасывается из рассмотрения.
2. Если же луч сферу пересекает, то группа дробится на более мелкие ассоциации, каждая из которых в свою очередь окружается сферой. Проверяется пересечение луча с каждой из этих сфер. Те сферы, которые луч не пересекает, выпадают из процесса. Оставшиеся дробятся более мелкими сферами дальше.
3. Количество проверок имеет логарифмический порядок от общего числа объектов.

Другой вариант применения той же идеи — разбиение не на сферы, а на полупространства, что несколько проще для реализации.
Все описанные вещи являются классическими и давно известны в своей области. Давайте поговорим немного о более актуальных вопросах, о новых идеях и разработках, которые также направлены на оптимизацию этого прекрасного процесса построения графики.

Актуальные проблемы
Трассировка лучей по сравнению с растровыми методами (таковым, например, является метод использования OpenGL, описанный в предыдущей статье) предоставляет результаты на порядок более высокого качества. Отсутствие дефектов, идеальная прорисовка всех оптических свойств должны были сделать этот алгоритм наиболее популярным. На самом же деле трассировка применяется весьма редко и только там, где качество визуализации — несравненно более важный критерий, нежели время выполнения. А это время для программ по трассировке огромно и достигает десятков и сотен часов. Это, конечно, не такая уж большая проблема, если целью является получение готового изображения или фильма. Но такое время абсолютно неприемлемо для обработки интерактивных приложений, а именно они нас чаще всего и интересуют. Поэтому вопрос об оптимизации алгоритма стоит очень остро и активно разрабатывается.
Здесь есть два основных направления оптимизации — за счет снижения качества либо с помощью использования суперкомпьютеров, параллельных вычислений и специальных свойств графических процессоров.
Что касается первого направления, то оно ведет к своеобразному слиянию трассировки с растровыми алгоритмами. Здесь есть следующие идеи:

1. Вначале растровыми средствами выстраивается весьма грубая картинка, а затем на нее сверху добавляются отдельные специальные эффекты методом трассировки. Например, можно трассировать только прозрачные объекты и те плоскости, на которые они отбрасывают свои цветные тени.
2. В анимации используется информация о предыдущем кадре. Вначале картинка строится только по сохраненной информации с учетом изменения угла обзора, расстояния до объектов и т.д. В новом кадре при этом возникают «черные дыры», или коллизии, обнаружение которых возлагается на небольшой эвристический анализ, который, к примеру, сравнивает яркость соседних пикселов, выставляя каждой точке изображения уровень «ошибочности», а затем для наиболее «ошибочных» пикселов вызывается новая трассировка.
3. Аппроксимация в процессе трассировки. Уменьшить количество обрабатываемых лучей можно, попросту интерполируя цвет пикселов по ближайшему окружению. Чтобы избежать дефектов, нужно прогнозировать расположение областей с высокой контрастностью и просчитывать их точно, без аппроксимации.

Существуют также механизмы оптимизации, не снижающие качества результатов, но большинство из них обеспечивают пока весьма скромный выигрыш по времени.
Это, во-первых, уже упоминавшийся механизм построения дерева, или графа объектов. Такая логическая структура позволяет существенно сократить число процедур, вызываемых для каждого луча, путем отбрасывания заведомо неуспешных. Во-вторых, ведутся работы по изучению самого механизма рекурсии, который, как известно, весьма неудобен для выполнения процессором. Эти исследования носят фундаментальный характер и призваны усовершенствовать алгоритм на уровне идеи, исключив из него рекурсию как таковую. Кроме того, можно попытаться более эффективно использовать те преимущества, которыми обладают современные графические процессоры, такие как большой объем кэш-памяти и различные расширения.
Наилучшие результаты предоставляет другой очень мощный подход — использование параллельных вычислений. Трассировка лучей будто специально создана для распараллеливания — ведь вычисление цвета каждого пиксела в алгоритме никак не связано с вычислением всех остальных. Так, в Университете шт. Юта создана интерактивная трассирующая система, которая использует параллельно 128 процессоров.
Интересный подход представляет собой объединение лучей в связанные пучки и обработка этих пучков параллельно. При этом как раз можно очень эффективно использовать расширения и увеличенную кэш-память современных процессоров.

Перспективы есть
В настоящее время алгоритм трассировки лучей развивается очень интенсивно, им занимаются как исследовательские институты, так и независимые программисты. Все это, безусловно, связано не только с эстетической ценностью поставляемых им плодов, но и с его мощным прикладным потенциалом во множестве различных областей. Я предлагаю вам попробовать эту вещь на практике и, возможно, внести свой вклад в ее развитие.

Редакция и автор статьи благодарят за предоставленные иллюстрации Александра Фокина («Метасферы») и Яна Торнтона («Стеклянные шахматы»)