Пользовательские функции (UDF), реализованные Microsoft в SQL Server 2000, обеспечивают возможность построения изящных программных решений при выполнении обработки данных. В рамках SQL Server, лишенного UDF, некоторые задачи слишком сложны и могут быть решены только на уровне клиентского приложения. Подобные решения подразумевают двусторонний обмен данными между клиентом и сервером даже тогда, когда пользователю нужны только результаты вычислений по базе данных. Одна из таких сложных проблем б- операции с комплексными (мнимыми) числами. Комплексные числа сами по себе являются мощным инструментом в решении многих математических задач, справиться с которыми посредством действительных чисел слишком сложно. Но если использовать UDF с поддержкой алгебры комплексных чисел, то нет нужды заботиться об этой математической сложности.
Стандартная форма представления комплексного числа: z=a+bi. Комплексное число z состоит из двух частей б- действительной (a) и мнимой (b), каждая из которых является действительным числом, а i б- квадратный корень из -1. Комплексные числа называют также мнимыми из-за того, что они дают решение уравнению i2=-1, чего нет в обычной алгебре. Однако если представить, что решение такого уравнения существует, т. е. действительно существует некое «число» i, равное квадратному корню из -1, то тем самым можно облегчить решение более сложных проблем. На самом деле мнимые числа занимают прочные позиции во многих областях (физика, медицина, электроника и др.).
 |
| Рисунок 1. Геометрическое изображение комплексного числа. |
Комплексным числам соответствуют простые геометрические образы на двумерной плоскости. В этом случае ось x называют действительной осью, ось y б- мнимой осью, а саму плоскость z б- плоскостью комплексных чисел, или z-плоскостью. Комплексное число изображают либо точкой с координатами (a, b), либо вектором с началом в центре координат (0, 0) и концом в точке с координатами (a, b) (см. Рисунок 1).
Зачем нужен T-SQL?
Комплексные числа требуют не только особого обращения, но и богатого воображения, поэтому арифметические операции и другие вычисления с комплексными числами представляют собой уникальную алгебру. В такой обюектно-ориентированной среде, как С++, например, поддерживать комплексные числа достаточно просто б- можно создать класс комплексных чисел. Можно даже загрузить арифметические операции сложения (+), вычитания (-), умножения (*) и деления (/), что сделает обращение с комплексными числами более естественным.
T-SQL, в отличие от С++, в настоящее время не поддерживает обюектно-ориентированные возможности, т. е. пользователь не может создавать классы, представляющие комплексные числа. Тем не менее в T-SQL есть две другие возможности б- либо хранить действительную и мнимую части как два раздельных значения, либо хранить комплексное число целиком как строку символов (например, 1+2i).
Неудобство при выполнении операций с комплексными числами в клиентском приложении состоит в том, что пользователю приходится иметь дело со всей совокупностью данных. T-SQL же обладает огромной мощью в обработке наборов данных, а кроме того, он возвращает только нужные клиентскому приложению результаты вычислений. Благодаря этому T-SQL и позволит найти подходящее решение. Несмотря на то что T-SQL не обладает свойствами обюектно-ориентированной среды, он позволяет писать UDF, которые можно включать в запросы, а такая возможность делает UDF идеальным инструментом T-SQL для обращения с комплексными числами.
Хранение и расщепление комплексных чисел
Выполнять действия с комплексными числами удобней, если хранить их в символьной строке переменной длины. Можно даже создать определяемый пользователем тип (UDDT), назвав его Complex, и использовать при описании переменных.
EXEC sp_addtype complex, 'varchar(50)'
При таком подходе прежде всего осуществляется проверка того, что всякое значение переменной, представляющей комплексные числа, задано корректно. Возможно, также понадобится выделить действительную и мнимую части комплексного числа с тем, чтобы производить вычисления, использующие лишь одну из этих частей.
Итак, перейдем к написанию программы. Первая задача б- построить функцию с аргументом типа символьная строка переменной длины, хранящей комплексные числа. Эта функция проверяет, является ли строка символов корректно заданным комплексным числом. Если да, то функция принимает значение 1, если нет б- значение 0. Программа в Листинге 1 представляет функцию с именем cxValid, которая и выполняет эту задачу. Функция cxValid производит ряд проверок входного параметра @cx, и, как только одна из проверок не проходит, выполнение программы прекращается. Сначала функция удаляет начальные и хвостовые пробелы. Поскольку функция рассматривает аргумент как входной параметр, любые действия над аргументом внутри функции не влияют на значение аргумента за ее пределами. Фактически входной параметр б- это лишь копия значения переменной, а не указатель адреса этого значения в памяти. Первый тест заключается в проверке крайнего правого символа строки б- это должна быть буква i. Если это так, программа удаляет крайний правый символ. Далее выполняется встроенная команда поиска символа по образцу (PATINDEX('%_[-+]',@cx)+1), для нахождения позиции знака + или б- в середине строки и дальнейшего сохранения ее в переменной @signpos. Эта команда поиска возвращает номер позиции символа, предшествующего знаку + или б-, который должен быть в середине комплексного числа. Затем добавляем 1 и получаем точное значение местоположения знака. Хочу отметить важность подчеркивания, которое соответствует одиночному символу. При этом, если действительная часть комплексного числа содержит собственный знак (-3, например), команда поиска игнорирует его, поскольку ей требуется хотя бы один символ перед знаком. Наконец, если в середине предполагаемого комплексного числа знака найдено не было, PATINDEX возвращает 0.
Теперь, когда номер позиции знака в середине строки сохранен в переменной, можно легко выделить действительную и мнимую части комплексного числа и проверить с помощью встроенной функции IsNumeric, являются ли они числовыми значениями. Если строка прошла все проверки, cxValid возвращает значение 1. Это означает, что данная строка символов является допустимым значением, в противном случае функция возвращает 0.
Если нужно, чтобы в столбцах заданного типа Complex были только корректно заданные комплексные числа, следует ввести правило, которое обеспечивает ту же логику, что и функция dbo.cxValid, а затем связать это правило с пользовательским типом Comp-lex. На Листинге 2 показано, как создается такое правило и как оно связывается с типом Complex. Обратите внимание, что функцию cxValid нельзя использовать внутри правила, потому что в правилах SQL Server допускается использование только встроенных функций. Кроме того, каждое правило должно быть записано как единое выражение, и значит, при задании правила не удастся разделить проверочную логику на несколько этапов, как в функции cxValid. Поскольку для хранения комплексных чисел используется символьная строка переменной длины, в представлении комплексных чисел появляется некоторая неоднозначность. Вот несколько допустимых вариантов записи одного и того же комплексного числа, демонстрирующих эту гибкость:
1+2i
1 + 2i
+1 + 2i
1.000+ 2.0i
Беспорядочная запись комплексных чисел выглядит некрасиво. А придерживаясь определенного порядка в записи комплексных чисел, можно упростить написание программ. Например, пользователь может указывать знак перед действительной частью только в том случае, если это минус, отделять с обеих сторон промежуточный знак одиночными пробелами, удалять начальные и хвостовые пробелы, а также удалять позиции с незначащими нулями. Можно задать функцию, аргумент которой б- корректно заданное комплексное число, а значение б- то же самое число, приведенное к стандартному виду [-]a{+/-}bi. Пример в Листинге 3 описывает функцию cxStandardize, которая выполняет следующие действия.
- С помощью встроенной функции REPLACE удаляет все пробелы.
- Отделяет друг от друга действительную и мнимую части (промежуточный знак остается с мнимой частью) и удаляет все позиции с незначащими нулями.
- Соединяет действительную и мнимую части, дописывая мнимую часть вслед за действительной.
- Вставляет одиночные пробелы перед промежуточным знаком и после него.
- Удаляет знак + перед действительной частью, если он есть.
Перед началом выполнения действий комплексной арифметики часто требуется выделить действительную и мнимую части комплексного числа. Снова для этой цели можно создать функцию. Листинг 4 содержит полное и весьма простое описание функций cxGetReal и cxGetImaginary. Эти функции используют встроенную функцию PA-TINDEX точно так же, как и предыдущие функции, б- они определяют номер позиции промежуточного знака и возвращают соответствующую часть строки либо по левую сторону от знака, либо сам знак вместе с тем, что по правую сторону от него, исключая букву i.
Помимо необходимости разбить строку, представляющую комплексное число, на ее действительную и мнимую части, может понадобиться и обратное б- составить комплексное число из данных действительной и мнимой частей. Функция cxStrForm в Листинге 5 компонует строку из четырех частей: действительной части, знака мнимой части, самой мнимой части и символа i. Действительная и мнимая части являются аргументами функции cxStrForm. Знак вычисляется при помощи встроенной функции SIGN(), где в качестве аргумента берется мнимая часть. Теперь для окончательного формирования строки, представляющей комплексное число, остается только записать одну за другой все эти части. Полученная строка передается в функцию cxStandardize в качестве аргумента, а та приводит исходное комплексное число к стандартному виду.
Более сложные операции с комплексными числами
 |
| Рисунок 2. Сложение комплексных чисел. |
Итак, фундамент заложен, и следующий шаг б- обеспечение программными средствами комплексной арифметики. У комплексных чисел есть свои правила сложения, вычитания, умножения и деления, и с помощью UDF можно обеспечить их выполнение.
 |
| Рисунок 3. Геометрическое изображение сложения комплексных чисел. |
Чтобы сложить два комплексных числа, следует сложить отдельно действительную и мнимую части (см. Рисунок 2). Геометрически сложение можно представить следующим образом (см. Рисунок 3). Если начертить параллелограмм, исходя из векторов складываемых комплексных чисел, то сумме соответствует диагональ параллелограмма, т. е. вектор с началом в начале координат и концом в противоположной вершине, при этом координаты вершины равны сумме координат исходных векторов.
 |
| Рисунок 4. Вычитание комплексных чисел. |
Теперь легко построить функцию cxAdd (см. Листинг 6). Функция имеет два аргумента типа комплексное число и производит вычисления в четыре этапа. Сначала используется функция cxValid. Она проверяет, являются ли оба аргумента корректно заданными комплексными числами, и, если хотя бы один из них таковым не является, функция cxAdd возвращает NULL. Затем используются функции cxGetReal и cxGetImaginary; выделенные из обоих аргументов действительные и мнимые части сохраняются в числовых переменных. После этого функция вычисляет суммы действительных и мнимых частей по правилам комплексного сложения. И в конце используется функция cxStrForm, которая возвращает результат сложения в стандартном виде комплексного числа.
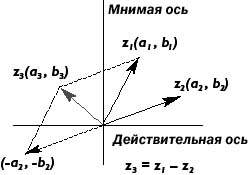 |  |
| Рисунок 5. Геометрическое изображение разности комплексных чисел. | Рисунок 6. Умножение комплексных чисел. |
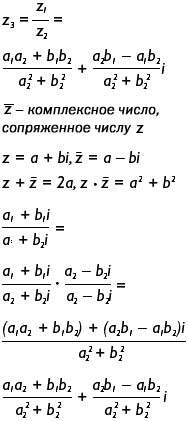 |
| Рисунок 7. Деление комплексных чисел. |
Комплексное вычитание производится почти так же, как и сложение. Действительная и мнимая части вычитаются отдельно, как показано на Рисунке 4. С геометрической точки зрения комплексное вычитание можно рассматривать как частный случай сложения: второе число берется с противоположным знаком и складывается с первым (см. Рисунок 5). В Листинге 7 приведено описание функции cxSubtract. Функция cxSubtract устроена так же, как и cxAdd. Единственное изменение должно быть внесено в формулу, дающую окончательные действительную и мнимую части.
На Рисунке 6 показано, как перемножаются два комплексных числа. Обратите внимание, что в определенный момент вычислений выражение b1b2i2 заменяется на b1b2 т.к.i2=-1. Результат комплексного умножения основан на предположении, что уравнение i2=-1 имеет решение, в противном случае формулу умножения было бы нельзя упростить.
В Листинге 8 дано описание функции cxMult. Как и в предыдущих случаях, устройство функции cxMult аналогично устройству других функций; меняются только формулы окончательной действительной и мнимой частей.
 |
| Рисунок 8. Полярная форма комплексного числа. |
Комплексное деление использует сопряжение комплексных чисел. Комплексное число, сопряженное числу z, обозначается _z; оно имеет ту же действительную часть, что и z, а его мнимая часть б- это взятая с обратным знаком мнимая часть z. Если умножить комплексное число на сопряженное ему, то получится a2+b2. При делении комплексных чисел числитель и знаменатель домножаются на a2-b2*i, т. е. делитель превращается в (a2+b2i)*(a2-b2i). Это выражение является произведением числа на сопряженное ему, и оно приводит к знаменателю a22+b22. Рисунок 7 поясняет, как производится комплексное деление. Листинг 9 содержит программу, которую можно использовать для создания функции cxDivide, и окончательные формулы действительной и мнимой частей.
Полярная форма комплексных чисел
 |
| Рисунок 9. Вычисление длины вектора. |
Комплексные числа представляют также в полярной форме (r, н?). Полярная форма используется в тех случаях, когда для вычислений имеет значение величина угла вектора, изображающего комплексное число. Первый компонент полярной формы (r) б- длина вектора, т. е. расстояние от начала координат до точки (a, b) на комплексной плоскости. Угол (н?) б- это угол между действительной осью и вектором, который представляет комплексное число. Полярная форма комплексного числа изображена на Рисунке 8. Длину вектора на комплексной плоскости называют также абсолютным значением или модулем. Длина вектора вычисляется по теореме Пифагора, как показано на Рисунке 9. На Рисунке 10 изображен треугольник с вершинами в точках (0, 0) (a, 0) (a, b). Согласно теореме Пифагора, длина r равна квадратному корню из суммы двух других сторон, возведенных во вторую степень. Итак, полярная форма комплексного числа: z=r*cosн?+i*r*sinн?. Из этой формулы выводится формула Эйлера (см. Рисунок 11), которая широко используется в комплексной алгебре. Пользуясь терминами полярной формы, можно написать UDF, которая вычисляет длину вектора r по теореме Пифагора (см. Листинг 10).
 |
| Рисунок 10. Геометрическое изображение модуля комплексного числа. |
Эти несколько примеров иллюстрируют общую идею того, как с помощью UDF обеспечивается комплексная алгебра. Отталкиваясь от элементарных функций, можно создавать другие комплексные функции, которые могут понадобиться в дальнейших построениях, например корень n-й степени из комплексного числа.
Что дают комплексные функции
| Рисунок 11. Формула Эйлера. |
Оперирование комплексными числами в SQL Server представляет собой не только хорошее упражнение в написании функций и в решении задач комплексной алгебры (да и вообще темой для более глубокого изучения), но и также практическое применение. При большом количестве комплексных чисел можно хранить их в таблицах, создавать запросы на поиск чисел, заполнять ими ячейки и ориентироваться среди записей, возвращаемых в клиентское приложение. Клиентское приложение не нуждается в том, чтобы хранить у себя такое огромное количество данных. Более того, некоторые приложения работают со сложными исходными данными большого обюема даже тогда, когда реально им нужны только обработанные результаты вычислений исходных данных. Обращение к готовым результатам вычислений сокращает цикл обмена данными между клиентом и сервером и позволяет задействовать возможности SQL Server в обработке данных с большей эффективностью. Для иллюстрации возможностей комплексных чисел предлагается метод применения комплексных функций в запросах. А во врезке «Обработка звука и изображения» приведен пример использования комплексных чисел в обработке звука и изображения.
Использование комплексных чисел
Для начала можно создать простую таблицу с двумя столбцами, в которых хранятся комплексные числа, а затем выполнить запрос к этой таблице. В примере Листинга 11 создается таблица ComplexNumbers, которая заполняется образцами комплексных чисел. Теперь для выполнения сложения, вычитания, умножения и деления с каждой парой нужно вставить в запрос комплексные функции (см. Листинг 12). В Таблице 1 содержатся результаты этого запроса. Каждая строка в результирующем наборе состоит из двух комплексных чисел и их суммы, разности, произведения и частного. Производить комплексные операции с числами, которые сами являются результатами вычислений, б- задача более сложная, нежели одинарные вычисления. Допустим, нужно подсчитать сумму произведений всех пар комплексных чисел из таблицы ComplexNumbers. Хотя система UDF насыщена разнообразными функциональными возможностями, T-SQL не позволяет создать функцию, которая работала бы со строками таблицы и которую можно было бы включить в запрос как любую другую встроенную функцию, например SUM(). Однако можно сделать следующий ход: T-SQL позволяет выполнять запросы с сохранением результата в переменной. Такой запрос не возвращает результат в клиентское приложение, а присваивает определенное значение некоторой переменной. Для этого следует задать переменную типа комплексное число и присвоить ей начальное значение 0+0i. Далее, запрос циклически обрабатывает все строки таблицы и всякий раз, переходя к очередной строке, добавляет к значению переменной произведение соответствующей пары комплексных чисел. В Листинге 13 содержится пример подобного запроса.
Те проблемы, которые были почти неразрешимы в предыдущих версиях SQL Server, стали простыми в SQL Server 2000 и UDF. Поэтому UDF можно использовать не только для манипулирования комплексными числами, но и для множества других задач в силу большой гибкости данного программного средства.
Ицик Бен-Ган б- старший преподаватель на курсах по SQL Server в колледже Hi-Tech в Израиле. Является председателем израильской группы пользователей SQL Server. С ним можно связаться по адресу: itzikb@hi-tech.co.il.
Обработка звука и изображения
Давайте теперь рассмотрим пример использования комплексных чисел в базах данных. Практическое применение этой абстрактной идеи до сих пор полностью не раскрыто. Этот пример касается данных, представляющих звуковые волны. Данные, представляющие звуковую волну, хранятся в таблице SQL Server, при этом каждая строка содержит показатель уровня звука в определенный момент времени (пространственная область значений). Такой способ хранения данных более удобен для создания звукового файла из табличных данных. Список команд, создающих таблицу SoundWave, может выглядеть так:
CREATE TABLE SoundWave ( time_index int NOT NULL PRIMARY KEY, sound_level decimal(19,9) NOT NULL )
Допустим, в этой таблице содержатся данные пятиминутного трека с компакт-диска. При частоте дискретизации 44,1 кГц таблица будет содержать 13 230 000 строк: 44 100 фрагментов в секунду * 300 секунд. Задача состоит в том, чтобы получить преобразованную звуковую волну с помощью данного фильтра из таблицы Filter (т. е. применить к исходному звуку определенные звуковые эффекты или эффекты эквалайзера) и сохранить звуковую волну в таблице FilteredSoundWave. Программа, создающая таблицу Filter, может выглядеть следующим образом:
CREATE TABLE Filter ( frequency_index int NOT NULL PRIMARY KEY, filter_vector complex NOT NULL )
Проблема состоит в том, что у данных в таблице Filter б- частотная область значений, тогда как у данных в таблице SoundWave б- пространственная. Поэтому перед применением фильтра к исходной звуковой волне нужно преобразовать звуковые данные к частотной области значений. Для этого используется математический алгоритм комплексного преобразования Фурье. В рамках данной статьи преобразования Фурье в деталях не обсуждаются, но будем считать, что к функциям, обеспечивающим преобразования Фурье, имеется доступ. Итак, к исходным данным применяется преобразование Фурье, а результат сохраняется в таблице TransformedSoundWave, созданной в следующей программе:
CREATE TABLE TransformedSoundWave ( frequency_index int NOT NULL PRIMARY KEY, filter_vector complex NOT NULL )
Каждая строка в таблице TransformedSoundWave содержит частотный индекс и комплексное число. Длина вектора комплексного числа выражает уровень сигнала, а угол вектора выражает сдвиг фазы сигнала. Теперь применение фильтра к исходной волне становится простым б- оно состоит в комплексном умножении векторов фильтра и векторов звуковой волны. Сохранить преобразованный звук можно в таблице TransformedFilteredSoundWave, имеющей частотную область значений. Структура этой таблицы такая же, как и у таблицы Trans-formedSoundWave. Для того чтобы сохранить звуковую волну, можно создать запрос (см. Листинг А).
Теперь полученный звук с наложенным эффектом следует преобразовать из частотной области значений обратно в пространственную, для чего используется обратное преобразование Фурье. Результат сохраняется в таблице FilteredSoundWave с такой же структурой, как и у таблицы SoundWave. Помимо сохранения всех промежуточных этапов обмена данными между клиентом и сервером, использование этого метода позволяет хранить и преобразовывать звук непосредственно в базе данных сервера. В дальнейшем, выполнив простую процедуру, из таблицы, содержащей звуковые данные, можно создать файл типа .wav.
Этот простой пример показывает, как можно использовать комплексные функции в базах данных. На практике, при выполнении определенных вычислений, вместо сохранения промежуточных результатов в таблицах можно использовать запросы, включая в них подходящие функции. Поэтому представленные выше промежуточные таблицы могут и не понадобиться. Подобную процедуру можно выполнить и для создания визуальных эффектов у исходных графических данных. В этом случае используются графические фильтры.
Листинг А. Наполнение таблицы параметрами преобразованной звуковой волны.
INSERT INTO TransformedFilteredSoundWave
SELECT
T.frequency_index,
dbo.cxMult(T.signal_vector, F.filter_
vector) AS signal_vector
FROM
TransformedSoundWave AS T
JOIN
Filter AS F ON T.frequency_index =
F.frequency_index| key_ col | cx1 | cx2 | Add | Subtract | Multiply | Divide |
| 1 | 5 + 2i | 2 + 4i | 7 + 6i | 3 - 2i | 2 + 24i | 0.9 б? 0.8i |
| 2 | 2 + 9i | 4 + 5i | 6 + 14i | -2 + 4i | -37 + 46i | 1.29268292 + 0.63414634i |
| 3 | 7 + 4i | 3 + 2i | 10 + 6i | 4 + 2i | 13 + 26i | 2.23076923 - 0.15384615i |
| 4 | 3 + 2i | 6 + 3i | 9 + 5i | -3 - 1i | 12 + 21i | 0.53333333 + 0.06666666i |
| 5 | 4 + 3i | 7 + 2i | 11 + 5i | -3 + 1i | 22 + 29i | 0.64150943 + 0.24528301i |
| 6 | 1 + 4i | 4 + 3i | 5 + 7i | -3 + 1i | -8 + 19i | 0.64 + 0.52i |
| 7 | 7 + 2i | 8 + 1i | 15 + 3i | -1 + 1i | 54 + 23i | 0.89230769 + 0.13846153i |
| 8 | 2 + 3i | 3 + 6i | 5 + 9i | -1 - 3i | -12 + 21i | 0.53333333 - 0.06666666i |
| 9 | 3 + 6i | 2 + 8i | 5 + 14i | 1 - 2i | -42 + 36i | 0.79411764 - 0.17647058i |
| 10 | 2 + 1i | 3 + 2i | 5 + 3i | -1 - 1i | 4 + 7i | 0.61538461 - 0.07692307i |

