При планировании деятельности ИТ-службы, как правило, используют либо метод учета затрат по видам деятельности (Activity-Based Costing, ABC), либо метод прямых затрат (Direct Costing).
При планировании деятельности ИТ-службы, как правило, используют либо метод учета затрат по видам деятельности (Activity-Based Costing, ABC), либо метод прямых затрат (Direct Costing). Эти методы не включают в рассмотрение качественные характеристики ИТ-услуг, о которых идет речь в соглашении об уровне обслуживания. Методы теории массового обслуживания позволяют связать качественные и количественные характеристики ИТ-услуг, что дает возможность более корректно планировать затраты ИТ-службы.
Задача планирования резервов
Основная задача планирования ресурсов для предоставления ИТ-услуг — это минимизация затрат при гарантированном качестве их предоставления и поддержки. Согласно рекомендациям ITIL [2], качество ИТ-услуг оговоривается в соглашении об уровне обслуживания. В частности, должны быть зафиксированы такие параметры, как время реакции Службы поддержки пользователей, время восстановления работоспособности ИТ-услуги, максимальная доля инцидентов, для которых время восстановления превышает оговоренное, и другие.
При планировании деятельности ИТ-службы необходимо оценить объем ресурсов, требуемых для обеспечения заданного уровня обслуживания. Справиться с этой задачей помогает моделирование процессов предоставления и поддержки услуг. Математическое моделирование этих процессов может быть выполнено с привлечением специального раздела теории вероятностей, который называется теорией массового обслуживания (ТМО). При корректном его применении на практике становится возможным связать качественные характеристики услуг и количественные параметры процессов предоставления и поддержки этих услуг: мощность серверов, число специалистов и т.д.
При разработке новых ИТ-услуг встает также вопрос планирования мощностей для предоставления услуги пользователям. Чтобы определить требуемые пропускную способность сети, дисковое пространство или процессорную мощность, нужно прогнозировать «спрос» на ИТ-услугу. При этом важно оценивать не только среднее число запросов в день, но и учитывать распределение пиковых нагрузок, возможность масштабирования ИТ-услуги и другие обстоятельства.
Менеджеры по планированию мощностей должны предусмотреть не только требуемые мощности, но и необходимые резервы — чтобы использовать их в моменты повышения нагрузки на ИТ-инфраструктуру.
Аналогичная задача ставится и при планировании поддержки ИТ-услуги. Планируя резервы трудовых ресурсов, необходимо учитывать отпуска, больничные, увольнения.
Корректно учесть эти нюансы можно, только имея статистику о работе службы поддержки в данной организации. Экономическая модель на основе ТМО удобна тем, что позволяет включать в рассмотрение различные виды ресурсов — как трудовых, так и материальных. Скажем, сервер, обрабатывающий запросы пользователей, и диспетчер, принимающий обращения по телефону, имеют много общего и могут рассматриваться как системы массового обслуживания.
Почему фактор случайности так важен
Большинство процессов поддержки ИТ-услуг носят случайный характер. Наиболее типичен процесс управления инцидентами, которые, по определению, происходят незапланированно. Поток звонков в службу поддержки пользователей представляет собой случайный процесс и характеризуется статистическими параметрами: средним числом звонков, распределением длительности промежутков времени между звонками. Логично, если планирование этих процессов учитывает их вероятностные характеристики и осуществляется на базе теории массового обслуживания (ТМО).
Типичное соглашение об уровне обслуживания, предлагаемое ITIL, изначально сформулировано в терминах ТМО. Характеристика ИТ- услуги включает время восстановления и долю инцидентов, устраняемых в оговоренный срок. Если рассматривать категорию качества обслуживания, то она не может быть выражена иначе, чем в терминах вероятности. Сбои работоспособности на практике возможны всегда, дело заключается в вероятности сбоя. С точки зрения инфраструктуры обслуживание с уровнем доступности сервисов 90%, 99%, 99,9% и 99,99% требует принципиально разных решений. Точно так же при поддержке ИТ-услуг уровень доступности сильно влияет на требования к наличию резервов ресурсов: инженеров поддержки, складских запасов и т.д. Требование избыточности ресурсов влияет на стоимость ИТ-услуги для бизнеса.
В рамках таких детерминированных моделей, как учет затрат по видам деятельности и метод прямых затрат, не происходит расчета резервов, необходимых для обеспечения качества услуги. На практике это делается «на ощупь» или не делается вовсе. В соглашении об уровне обслуживания может быть указана мало к чему обязывающая в условии отсутствия статистики формулировка «90% инцидентов», либо пункт о качестве обслуживания может быт просто опущен. С ростом корпоративной культуры и стандартов будут ужесточаться и требования бизнеса к качеству ИТ-услуг, которые должны фиксироваться в соглашении об уровне обслуживания. Этому должно способствовать и развитие рынка аутсорсинга ИТ-услуг. Натуральные показатели процессов поддержки и предоставления ИТ-услуг можно рассчитать на базе модели затрат по видам деятельности, включив в планирование элементы ТМО.
Еесть еще одна важная причина для рассмотрения вероятностного аспекта предоставления ИТ-услуг. Она заключается в изменении относительного уровня резервов при расширении масштаба предоставляемых услуг.
Пусть изначально десять инженеров поддерживали работу ста пользователей, а теперь будет поддерживаться тысяча. Требуемое количество инженеров поддержки возрастает не пропорционально числу систем.
Это объясняется тем, что событие, когда одновременно заняты все инженеры, во втором случае намного менее вероятно, чем одновременная их занятость в первом случае. Поэтому обычно с ростом числа систем требуется меньше людей в расчете на одну поддерживаемую систему. При увеличении масштаба процесс поддержки становится более предсказуемым, особенно если инциденты происходят независимо, то есть один инцидент редко влечет за собой череду других.
И хотя уровень обслуживания не изменяется, нагрузка на инженера возрастает. Это не влечет увеличения численности персонала, поскольку рост нагрузки обусловлен сокращением ожидания нарядов на работу.
Зачем это нужно…
Предлагаемая модель учета, основанная на ABC-методе [1], наследует все его преимущества, прежде всего точный учет затрат в разрезе ИТ-услуг и ИТ-решений. Но рассмотрение вероятностного фактора добавляет к этому следующие возможности.
- Связь качества ИТ-услуги и ее стоимости. Соглашение об уровне обслуживания формулируется в терминах доступности, скорости реакции, доли обработанных в срок заявок и скорости восстановления ИТ-услуги. Иногда заказчик требует пересмотра этих характеристик. Тогда встает вопрос: как изменятся натуральные показатели процесса поддержки ИТ-услуги и ее себестоимость? Единственная альтернатива ТМО в этом случае — интуитивное принятие решения. Автор не отрицает важности интуиции менеджеров, но количественные расчеты повышают как надежность, так и убедительность предлагаемых решений.
- Принятие решений при масштабировании сервиса. При увеличении масштаба услуги, а тем более ее качества, требуемое количество ресурсов изменяется нелинейно. Например, увеличение числа пользователей в десять раз может привести к расширению системы поддержки пользователей всего лишь в три раза. Игнорирование этого факта может приводить к систематической ошибке при планировании в сторону завышения объема ресурсов и, как следствие, себестоимости ИТ-услуг. Использование ТМО поможет значительно точнее ответить на вопрос: сколько дополнительных ресурсов нам понадобится.
- Анализ рисков. Собранная при разработке модели информация используется для анализа рисков. Например, временной профиль нагрузок на серверы в совокупности со статистикой инцидентов в разрезе элементов конфигурации может дать понимание «узких мест» поддерживаемой системы.
- Оценка и выбор ИТ-решений. Анализ статистики инцидентов помогает точнее прогнозировать расходы на эксплуатацию различных ИТ-решений, что может быть полезно при анализе вариантов.
- Принятие решений об аутсорсинге. Приведенная модель полезна при передаче ИТ-услуг в аутсорсинг, поскольку модель позволяет точнее рассчитать себестоимость поддержки, При этом себестоимость может быть различной для заказчика и провайдера услуг за счет экономии последнего на масштабе.
... и сколько это стоит
Движение от учета прямых затрат к учету затрат по видам деятельности приводит к росту издержек за счет дополнительного персонала и усложнения собираемой информации. Расчет вероятностных затрат стоит еще больше. Есть два фактора, которые увеличивают стоимость использования этой модели: необходимость сбора информации об инцидентах с учетом времени и использование математического аппарата теории вероятностей.
Для ABC-модели достаточно узнать число зарегистрированных инцидентов в разрезе ИТ-услуг, чтобы разнести себестоимость, при использовании ТМО необходима статистика времени возникновения и разрешения инцидентов. Второй фактор, увеличивающий стоимость использования модели, — это необходимость использовать довольно сложный математический аппарат. В отличие от элементарных методов учета, вероятностная модель учитывает качество услуг, выраженное в вероятностных величинах. Даже используя инструментарий имитационного моделирования, приходится создавать модель под каждый конкретный случай.
Какая информация требуется для использования модели, например для процесса управления инцидентами? Сначала приведем информацию, необходимую для расчета себестоимости ИТ-услуги по ABC-модели:
- регламент процесса управления инцидентами — роли, процедуры, ресурсы;
- стоимость и нормативы использования оборудования;
- штатное расписание, нормативы трудозатрат, тарифная сетка работников;
- накладные расходы процесса — аренда, связь, управление;
- нормы расходов запасных частей и расходных материалов.
Какая же дополнительная информация нужна, чтобы можно было рассчитать характеристики вероятностной модели? Прежде всего нужно проанализировать временной разрез имеющейся статистики. Ниже приведена информация, требующаяся для планирования процесса управления инцидентами:
- статистика времени регистрации инцидента оператором службы поддержки, времени ожидания в очереди, времени разрешения инцидента, в разрезе уровня линии поддержки;
- политики и регламенты в области обработки инцидентов — правила эскалации инцидента, приоритеты пользователей при работе над инцидентами.
Обычно эти данные собирают на начальном этапе проекта, используя регламенты и базу данных системы Service Desk. Вероятностная модель может быть полезна только для организаций с высоким уровнем зрелости процессов ИТ-службы, поскольку требуется наличие действующих регламентов.
Экономическая оценка эффекта стандартизации
Демонстрируя изложенный подход, рассмотрим условный пример оценки эффекта от стандартизации корпоративных персональных компьютеров сквозь призму планирования резервов службы поддержки.
Предположим, что в организации исторически существуют три основных платформы для настольных компьютеров (назовем их условно А, B и C). Компьютеров типа А имеется 350, типа B — 250, а типа C — 200. Предположим, что платформы имеют одинаковые параметры надежности. В среднем на разрешение инцидента требуется один час, а инциденты с одним компьютером происходят в среднем один раз в две недели. Допустим, что инциденты происходят только в рабочее время, тогда вероятность появления сбоя составит 1/10*8 раз в час. В таком случае мы можем найти среднее число заявок, поступающих за один час. Для этого нужно число поддерживаемых систем умножить на вероятность выхода из строя одной системы: I=350+250+200/10*8=10 заявок в час.
Предположим, что для обслуживания систем требуются узкоспециализированные инженеры, способные работать только с одной платформой. Пусть по условиям обслуживания максимальное время от поступления заявки до начала работы над ней не должно превышать 0,5 часа, а в соглашении об уровне обслуживания зафиксировано, что 99% заявок требуется обслуживать в установленные 0,5 часа.
В этом случае мы получаем сформулированную задачу теории массового обслуживания. При наличии трех разных платформ требуется решить задачу для трех потоков разных заявок. Интенсивность первого потока составляет: I=350/10*8=4.375 заявок в час.
Учитывая, что среднее время на обслуживание один час и максимальное время ожидания 0,5 часа, можно найти требуемое число инженеров для обеспечения уровня обслуживания 99%. Для этого, при выполнении определенных предпосылок, используют формулу Эрланга С. Согласно расчетам для обеспечения требуемого качества обслуживания платформы А нам нужно девять инженеров. Аналогично можно найти требуемое число инженеров для других платформ: для B — 7 человек, для С — 6 человек. Требуемое число инженеров для обслуживания стандартизированных систем — 15 человек. Это меньше, чем требуемые 22 специалиста для трех разных платформ.
Данное явление объясняется снижением резервов, необходимых для нормального обслуживания. При независимом случайном появлении заявок мы можем столкнуться с ситуацией, когда в систему поступило количество заявок больше обычного. Чем меньше поток заявок, тем вероятнее появление событий, при которых в систему поступает, например, в два раза больше заявок, чем ожидалось. Для нескольких небольших потоков заявок резервов требуется больше (до 50%), чем при обслуживании одного однородного потока заявок, когда относительное количество резервов может составлять 3-5%. Ээто справедливо для независимого появления заявок в системе. В реальности оказывают влияние другие факторы: сезонное изменение интенсивности поступления заявок, риски одновременного появления заявок на обслуживание в результате вирусной атаки, инфраструктурного сбоя или других проблем.
Помимо планирования требуемых резервов под обслуживание, мы должны учитывать, что реальное количество работников должно превышать теоретически рассчитанное. Реальным работникам требуются обеденные перерывы, отпуска, больничные, обучение. Поэтому необходимо резервировать дополнительные места. В зависимости от размера службы поддержки этот коэффициент может изменяться. Имея статистику, можно рассчитать коэффициент дополнительного резервирования, но для простоты предположим, что он равен 20%. Тогда требуемое количество составит: 18 и 11+9+8=28 специалистов соответственно.
Принимая ставку заработной платы (с учетом социального пакета, налогов и отчислений) для инженеров поддержки равной 1200 долл., можно рассчитать экономический эффект от снижения расходов на поддержку при стандартизации систем. Он составит: (28 - 18) *1200*12 = 144 000 долларов в год. Как видим, эффект от стандартизации для компании значительный.
Можно оценить экономическое решение о переходе на единый корпоративный стандарт. При себестоимости пользовательских компьютеров 600долл., проект по замене систем B и С на платформу A будет стоить: (250+200)*600 = 270 000
Учитывая экономию на поддержке, при внутренней ставке дисконтирования 15%, этот проект окупается за 27 месяцев. При менее жестких требованиях к уровню обслуживания заказчика эффект будет значительно меньше.
Помимо эффекта экономии на поддержке, в пользу стандартизации говорят и меньший объем склада запасных частей и расходных материалов, а также экономия при оптовых закупках систем.
Литература
- Скрипкин К.Г. Экономическая эффективность информационных систем, М.: ДМК-Пресс, 2002.
- Service Support (IT Infrastructure Library Series), Stationary Office, ISBN 0113300158.
Василий Петреченко — независимый эксперт, vpetrechenko@yandex.ru
Формула Эрланга С
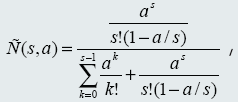
где C — вероятность того, что объект становится в очередь, s — число серверов, a — плотность входящего потока в Эрлангах.
Математическое моделирование
Теория массового обслуживания — это раздел теории вероятностей, посвященный изучению систем обработки заявок, имеющих случайную природу. В ТМО под заявкой понимают объект, который поступает в систему и требует времени на его обработку. Под сервером обычно понимается оператор, канал связи или другие ресурсы, занимаемые заявками и блокируемые на время обработки (см. рисунок) .
Аппарат теории массового обслуживания разрабатывался со времени появления телекоммуникаций как отрасли. Научные работы, положившие основание ТМО, принадлежат Агнеру Крарупу Эрлангу — сотруднику Копенгагенской телефонной компании. Формулы Эрланга B и С используются повсеместно при расчетах достаточной пропускной способности сети.
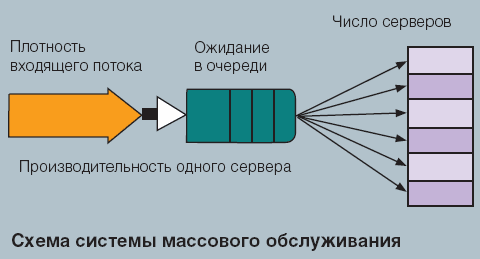
Система массового обслуживания характеризуется тремя основными параметрами: интенсивностью входящего потока, производительностью сервера и числом серверов в системе. Если бы заявки поступали в систему и покидали ее в строго определенные моменты, то система работала бы без очередей. В реальности возможно одновременное появление многих заявок в системе. В этом случае они становятся в очередь, откуда другое название ТМО: теория очередей.
Основная задача ТМО — определить вероятность того, что заявка будет обслужена вовремя. Обычно в ТМО рассматривается максимальное время ожидания заявки в очереди, но можно рассчитать и полное время на обработку заявки. На практике интерес представляет обратная задача: рассчитать число серверов, необходимых для поддержания требуемого уровня обслуживания.
Использовать ТМО, как и любую теорию, необходимо с оглядкой на адекватность предпосылок. Для корректных расчетов требуется большой объем статистики и тестирование гипотез о характере моделируемой системы. И все же имеющийся инструментарий имитационного моделирования позволяет решить большое число задач, встречающихся на практике.

