Из какого сора выросли ИТ?
Форма мысли, заключенная в названии раздела, не случайно «позаимствована» у великого поэта Анны Ахматовой. Ведь и замечательное упомянутое трио принадлежало к плеяде созидателей, которые наряду с Норбертом Винером, Клодом Шенноном, Аланом Тьюрингом и другими, стали родоначальниками важнейших направлений в развитии ИТ. Попробуем представить через их же достижения, что предопределило формирование интереса к ИТ.
Начать следует с того, что человечество уже в начале XX века столкнулось с огромными объемами информации, которые следовало превратить в знания, используя для этого более совершенные способы обработки, чем те, которые были известны. Информация поступала из самых разных сфер деятельности людей — от политических и социальных структур (бесконечные военные конфликты и первые национальные переписи, например), по научным и технологическим достижениям (в результате развития производства и использования электрической энергии, радиосвязи, появления автомобильной и авиационной промышленности), а также из бурно развивавшихся СМИ.
Еще одной причиной интереса к ИТ стали успехи в технологиях, активно стимулировавшиеся научными достижениями. Можно взять для примера бурное развитие физики, приведшее к разработке практических методов для создания средств связи и многих других технических средств.
Наконец, интеграционное воздействие названных причин, а также государственных и частных интересов, привело к широкому практическому использованию прикладных систем. Среди них были энергетические системы с дублированием мощностей, системы управления артиллерийским зенитным огнем, вычислительные системы (конечно, скорее вычислительные устройства, но с их помощью уже решали серьезные задачи) аналогового типа, защищенные линии связи и многие другие.
Стремление продвинуться в понимании этих явлений и стало важным стимулом в научной и практической жизни многих ученых и инженеров первой половины XX века. Среди них были и Колмогоров, и Марков, и Нейман.
Математика и ИТ
Все трое — выдающиеся математики прошедшего столетия, их вклады в развитие математической науки огромны. Занимаясь основаниями математики, они заложили фундамент для аксиоматических теорий информации, алгоритмов, вычислительных машин и квантовой механики, и получили в них глубокие результаты, опираясь в значительной мере на собственные достижения в различных областях этой науки.
Неслучайно, что среди пионеров, формировавших исходные представления об ИТ, были выдающиеся математики. Используя возможности фундаментальной науки, они предлагали инструментарий для количественных моделей процессов и систем, позволявший эффективно оценивать их практическую реализацию. При этом существенно, что получаемое решение не было единичным. Оно могло масштабироваться на ряд практических реализаций, его можно было оптимизировать в рамках избранной модели. Чтобы еще раз убедиться в этом, достаточно вспомнить модель вычислительной машины фон Неймана, определяющую до настоящего времени структурные представления цифровых вычислительных машин (рис. 1). Все это дало важное преимущество использованию ИТ.
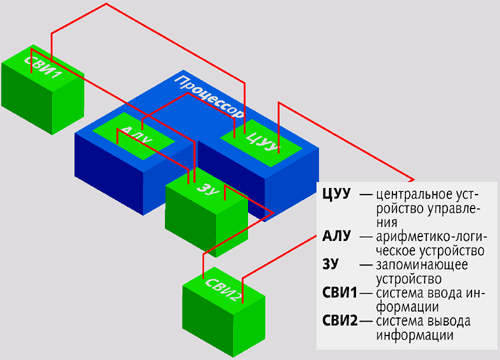
Рис. 1. Архитектура, предложенная Джоном фон Нэйманом
Понимание физических процессов и переход к технологическим решениям создания устройств и систем для обработки информации привели к бурному развитию самой математики и особенно ее прикладных разделов. Так, теория вероятностей выросла из математического раздела теории меры и стала фундаментом для теории информации, связи, систем управления и многих других дисциплин. Благодаря работам Колмогорова и его учеников, в теории информации были предложены строгие методы, которые позволили исследовать не только стационарные случайные процессы, но и марковские, а также обобщенные. Более того, использовать представления теории информации при решении собственно математических задач — таких, как описание свойств устойчивости динамических систем или структуры функциональных пространств, а также для характеризации случайной последовательности через ее сложность, а самой сложности через количество информации. Построение основ спектральной теории стационарных последовательностей — параллельно с Винером — дало толчок широкому развитию расчетных методик для приложений. Исследования по математической статистике привели Колмогорова к разработке методологии проверки гипотез и правил принятия решений на ее основе. Во время Великой Отечественной войны на этой базе ему удалось подготовить рекомендации для организации эффективной стрельбы зенитных орудий способом заградительного огня.
Колмогоров продолжил статистические исследования текстов, начатые А.А. Марковым (ст.), привнеся в них теоретико-информационные представления, в частности, критику попыток непосредственного использования математической теории информации.
Джон фон Нейман, участвуя в американском атомном проекте, предложил метод статистических испытаний Монте-Карло для решения на вычислительной машине расчетных многомерных задач математической физики. Но, пожалуй, существенно более важными стали его работы «Вероятностная логика и синтез надежных организмов из ненадежных компонентов» и «Теория игр и экономическое поведение». Первая определила идеологию и практику построения надежных устройств и систем — главнейшее направление использования ИТ. Тогда как вторая до настоящего времени остается фундаментальной работой при построении и анализе системных моделей, начиная с фирмы и кончая мировой экономикой — одно из перспективных направлений для ИТ в условиях глобализации последней.
Работы по математическим основаниям, которые выполнили Колмогоров, Марков и фон Нейман, позволили не только продвинуться в понимании того, что такое вычислительная машина в целом, предложив для этого различные математические модели, в том числе автоматы, но указать на алгебраические и вероятностные способы их анализа. Колмогоров и Марков уделили большое внимание созданию теории алгоритмов, а Марков даже написал известный труд «Теория алгорифмов» и развил направление конструктивной математики, положившее начало весьма популярной современной ветви теории вычислений, которая рассматривает алгоритмы, позволяющие решать задачи за конечное число шагов или за полиномиальное время.
Рассмотрение вычислительных процессов, как последовательности аксиоматически задаваемых операций, позволило не только оценивать структурную сложность вычислительных машин, но и их производительность, что стало важнейшей характеристикой в ИТ. В работах Колмогорова и его учеников были получены результаты по оценке сложности реализации алгоритмов для ряда операций. Более того, им и его учеником Владимиром Арнольдом была решена одна из известных проблем Гильберта о возможности представления функции многих переменных через суперпозицию функций двух переменных с использованием логических операций. Эта задача очень важна для ИТ, поскольку открывает принципиальные возможности по свертыванию или более экономному представлению информации. Марковым были написаны работы, содержащие примеры математических объектов, которые не могут быть построены за конечное число алгебраических операций, выбранных из определенного базиса.
Нейман, опираясь на возможности использования вычислительных машин для решения конкретных задач, предложил эвристический подход, который жив до сих пор и на слуху у тех, кто озабочен проблемами спама. Суть подхода состоит в получении в ходе численного эксперимента данных для уточнения исходной модели интересующего нас явления. В ходе разработки атомного и водородного оружия и в США, и в СССР такой подход был очень популярен и в дальнейшем привел к бурному развитию численных методов решения дифференциальных уравнений на цифровых вычислительных машинах и оказал огромное влияние на их совершенствование.
Интересно, что разработка эвристической методологии привела фон Неймана к необходимости разделения процесса программирования задачи на два этапа. В ходе первого этапа, в результате постановки задачи, составляется блок-схема программы. Далее, на втором этапе, она переписывается в кодах вычислительной машины.
Последнее, о чем в этой короткой заметке следует сказать, — это перспективы ИТ, которые виделись этим великим подвижникам науки. Разумеется, их занятия автоматами следовали из представлений, что универсальные вычислительные машины рядом с человеком во многом проигрывают и, в частности, процесс мышления не сводится к вычислительным операциям (кстати, на этом особый акцент делает известный современный британский ученый Роджер Пенроуз).
 |
|
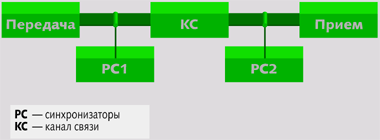
Для надежной работы КС 1. Часть пропускной способности КС отдается под постоянную синхронизацию связи в течении сеанса 2. В начале сеанса связи производица передача синхропосылки для заполнения РС2 надежной информацией 3. В течение сеанса производится регулярная проверка синхронности связи Рис. 2. Пример надежной схемы из ненадежных элементов |
Поэтому крайне интересное направление развития ИТ, связанное с эвристическим подходом к исследованию мозга и искусственного интеллекта путем моделирования на вычислительных машинах, захватило фон Неймана в заключительный период его жизни. Книга, над которой он работал в последние годы, и которую ему не суждено было закончить, называлась The Computer and the Brain. Нейман отмечал, что интересно соотношение между центральной нервной системой и универсальными вычислительными машинами. Они различны по числу и порядку размещения элементов и по скорости выполнения операций. Имеются принципиальные отличия по логической организации мозга и машин, определяемые характером решаемых задач. Так, если машины работают в основном последовательно, то мозг — в значительной мере параллельно. В 1960 году в первом выпуске «Кибернетического сборника» был опубликован перевод его лекции на Силлимановских чтениях. В ней он сослался на подход Алана Тьюринга, предложившего моделировать одну вычислительную машину с помощью другой, что и позволило предложить критерий проверки интеллектуальности действий машины.
Нейман положил начало исследованиям по самовоспроизводящимся автоматам, что пробудило большой интерес к проблемам эволюции живого и, в частности, к тому, что есть жизнь. Появилось много направлений в биологических науках: от информационных представлений важнейших процессов до наследственной информации, а сегодня одна из требовательнейших к ресурсу вычислительных задач — установление состава генома человека.
Теперь обсуждение подобных проблем — удел философов. Действительно, миновали времена, когда Колмогорову необходимо было выступать в журнале «Техника — молодежи» со статьей «Автоматы и жизнь» или делать доклад на тему «жизнь и мышление с точки зрения кибернетики» на теоретической конференции семинаров научных учреждений АН СССР.
Их наследие
Эти три математика сделали столь много, что чужим пером не описать, поэтому их следует неспешно перечитать, а некоторым и прочитать. Этому послужит краткий перечень доступных работ.
А.Н. Колмогоров
Избранные труды, тома — Математика и механика, Теория вероятностей и математическая статистика, Теория информации и теория алгоритмов. — М.: Наука, 1985, 1986, 1987 гг.
А.А. Марков
Избранные труды, том II. — М.: МЦНМО, 2003 г.
Джон фон Нейман
Теория игр и экономическое поведение. М.: Наука, 1970 г.
Теория самовоспроизводящихся автоматов. М.: Мир, 1971 г.
Общая и логическая теория автоматов. В кн.: А. Тьюринг. Может ли машина мыслить? — М.: Физматгиз, 1960 г, с. 59-102.
Вероятностная логика и синтез надежных организмов из ненадежных компонентов. — В сб.: Автоматы. — М.: ИЛ, 1956, с. 68-139.
Collected Works? V. 1-6. — New York, Oxford, London, Paris: Pergamon Press, 1961-1963.
The Computer and the Brain. — New Haven: Yale University Press.
Кто они?

А.Н. Колмогоров (1903-1987)
Андрей Николаевич Колмогоров родился в Тамбове в семье ученого агронома и дочери ярославского помещика, предводителя дворянства города Углич. С 1920 года и до конца дней его судьба связана с Московским университетом. Он был профессором университета и членом АН СССР, а также многих других отечественных и зарубежных научных обществ. В значительной мере его трудами создана московская вероятностная школа, в которой и было выполнено много исследований по математической теории информации.

А.А. Марков (1903-1984)
Андрей Андреевич Марков родился в семье математика, члена Российской академии наук, который дал ему домашнее воспитание. С 1919 года и до переезда в Москву он был связан с Петроградским, а затем Ленинградским университетом, где создал замечательную школу конструктивного анализа. После переезда в Москву и до конца своих дней возглавлял кафедру математической логики Московского Государственного университета им. Ломоносова. Им была создана отечественная школа конструктивного анализа.

Джон фон Нейман (1903-1957)
Янош (Иоганн и, наконец, Джон) фон Нейман родился в семье банкира. Получил домашнее и очень хорошее гимназическое образование в Будапеште. Учился в знаменитом Цюрихском политехникуме, работал в университетах Гамбурга, Берлина и в Принстонском институте перспективных исследований. Принимал активное участие в Манхеттенском проекте и в работах по созданию первых ЭВМ. Выполнил множество выдающихся работ по математике и ее приложениям, оставил глубокий след во многих областях науки и техники.


