К наиболее трудоемким задачам медицины относятся постановка диагноза и выбор курса лечения. Традиционно врачи решали эти задачи, полагаясь лишь на собственную интуицию и опыт. Сегодня в их арсенал все чаще входят способы, основанные на высоких технологиях и позволяющие обрабатывать большие потоки информации.
Сегодня ИТ применяются в медицине по трем направлениям:
- использование оборудования для хирургического лечения, наблюдения больного в предоперационный и послеоперационный периоды и т.п.;
- ведение документооборота и финансово-бухгалтерской отчетности;
- прогнозирование состояния организма, диагностирование заболеваний, отслеживание стадий развития рецидива, назначение необходимого курса лечения с помощью интеллектуальных систем принятия решений.

Попытаемся проанализировать состояние дел в третьем, наиболее наукоемком направлении. Создаваемые в нашей стране и за рубежом экспертные системы и системы искусственного интеллекта, предназначенные для диагностирования, позволяют решать самые разные задачи. Эти задачи могут быть и очень узкими (например, составление графика эффективного приема определенных лекарственных препаратов для конкретного пациента), и более глобальными, связанными с прогнозированием состояния пациента, выдачей рекомендаций на хирургическое вмешательство и анализом возможного состояния больного в послеоперационный период. В зависимости от назначения такие системы базируются на различных методах; в их числе:
- статистические методы обработки данных (СМОД);
- искусственные нейронные сети (ИНС);
- нелинейные регрессионные методы (НРМ);
- рассуждения на основе аналогичных случаев (РОАС).
Статистические методы обработки данных
СМОД давно завоевали популярность как методы обработки информации, получаемой практикующими врачами [1]. Существует даже своеобразный регламент использования в научных публикациях того или иного способа обработки данных, различных критериев оценки полученных результатов, их оформления в текстовом и графическом виде. Наиболее часто применяются такие статистические методы обработки данных, как расчет критериев Стьюдента и Пирсона, коэффициентов корреляции и линейной регрессии и т.п.
Одна из задач статистического анализа данных — это нахождение взаимосвязи между явлениями. Для определения ее степени используют корреляционный анализ. Определив величину коэффициента корреляции, необходимо оценить направление связи (прямая или обратная), силу и достоверность полученного коэффициента. Кроме того, устанавливается уровень значимости коэффициента корреляции.
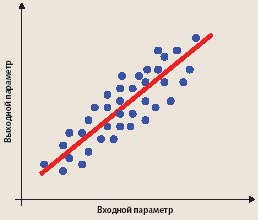
Для определения количественного изменения величины одного признака по мере изменения другого служит метод регрессии. Установленный с его помощью коэффициент регрессии позволяет по величине одного признака определять среднюю величину другого (см. рис. 1). Для этого необходимо построить элементарную математическую модель процесса, являющегося объектом исследования.
|
| Рис. 1. Поле корреляции и подходящая линия регрессии |
Часто медикам, исследующим реакцию организма на воздействие какого-либо раздражителя (заболевания или лекарственного препарата), приходится сравнивать результаты, которые относятся к исследуемой и контрольной группам, для того чтобы доказать не только различия, но и достоверность этих результатов.
В некоторых случаях указанные методы обработки данных дают неплохие результаты. В частности, при исследовании круга препаратов, характеризующихся предпочтительным уровнем переносимости и безопасности при использовании пациентами с теми или иными заболеваниями, статистические методы позволяют «увидеть» результаты проделанной работы. Часто для этого применяется пакет Statistica, обеспечивающий анализ результатов и их отображение в графическом виде.
Искусственные нейронные сети
Среди медиков пользуются популярностью специализированные нейронные сети, функционирующие по различным алгоритмам. Такие ИНС имеют достаточно простые в реализации схемы и структуры, позволяют точнее отразить связь между входными и выходными параметрами, требуют меньше усилий для настройки. Основу каждой ИНС составляют относительно несложные, обычно однотипные элементы (ячейки), в какой-то степени аналогичные нейронам мозга.
Каждый нейрон характеризуется его текущим состоянием, имеет группу синапсов (однонаправленных входных связей, соединенных с выходами других нейронов) и аксон (выходную связь, по которой сигнал возбуждения или торможения поступает на синапсы следующих нейронов). Синапс характеризуется величиной синаптической связи, которая эквивалентна электрической проводимости. Текущее состояние нейрона определяется как взвешенная сумма его входов.
Принцип работы ИНС состоит в параллельной обработке сигналов, которая достигается за счет объединения большого числа нейронов в так называемые «слои», а также соединения нейронов различных слоев и, в некоторых конфигурациях, нейронов одного слоя между собой (причем обработка взаимодействия всех нейронов ведется послойно). Теоретически число слоев и нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера. Некоторые разработчики утверждают, что увеличение числа слоев и нейронов в них не влечет за собой улучшения качества работы ИНС, а иногда даже, наоборот, приводит к ухудшению характеристик [2]. Поэтому для точного определения количества слоев и нейронов требуется доскональное исследование параметров процесса, подлежащего моделированию посредством ИНС.
Для решения некоторых типов задач уже разработаны и успешно применяются определенные конфигурации сетей (например, нейронные сети Хопфилда и Хэмминга). Если же задача не сводится ни к одному из известных типов, необходим синтез новой конфигурации. Возможности сети возрастают с увеличением числа ячеек, плотности связи между ними и количества выделенных слоев, но при неограниченном расширении сети есть вероятность ухудшения ее работы. Сложность алгоритмов функционирования сети также способствует увеличению мощи ИНС, но всякая сложность должна быть обоснована.
Положительной стороной ИНС, как отмечается в [2], является сравнительно небольшая выборка данных, предназначенных для обучения работе со сконструированной сетью, — вплоть до единственного случая для каждого возможного значения параметра. Это значительно облегчает сбор экспериментальной информации и ее подготовку к обработке.
ИНС используются для решения большого круга задач.
Прогнозирование риска осложнений в послеоперационный период. Например, в Пензенской областной больнице были проведены исследования. После выбора оптимального метода построения сети, а также оптимального числа слоев и синапсов был получен результат прогнозирования, обеспечивающий всего 12% ошибок.
Диагностирование и прогнозирование состояния сердечно-сосудистой деятельности пациентов. В 80-х — начале 90-х годов в Германии были разработаны нейронные сети с использованием разнообразных архитектур и алгоритмов функционирования, предназначенные для диагностики заболеваний сердца. Сравнение результатов тестирования ИНС с данными прогнозирования, полученными с помощью логического алгоритма, показали преимущество нейросетевого метода (диагностическая точность — 79%). Целый ряд исследований подтверждают положительный опыт применения ИНС для прогнозирования в кардиологии [3].
Диагностика и лечение артериальной гипертонии. Соответствующая нейросетевая система была разработана в Италии.
Ранняя диагностика раковых заболеваний с высокими показателями точности.
Нейронные сети использовались и в таких областях, как прогнозирование последствий аллергических реакций организма, обработка анализов крови, оценка вероятности смертельного исхода для конкретного человека в ближайшие десять лет и др.
Для проектирования ИНС используются специализированные и подручные средства — MATLAB, таблицы Paradox от Deqisy Software, различные языки программирования и т.п. Специалисты из красноярского ВЦ СО РАН, КГТУ, Красноярской медицинской академии, ряда клинических учреждений города и местного вычислительного центра СО РАН создали специализированный пакет программ MultiNeuron, при работе с которым не требуется помощь математиков и программистов.
Нелинейный регрессионный метод
НРМ требует более глубоких математических знаний, поэтому не столь часто используется в медицине. Одна из разновидностей НМР — метод группового учета аргументов (МГУА). Он нашел применение в самых разных областях, в которых используется структурная или параметрическая идентификация при прогнозировании. Пригоден он и для решения задач, связанных с результатами работы исследователей-медиков.
Ранее считалось, что точность модели можно повысить исключительно благодаря учету множества факторов и их композиции. Но такой подход требовал все большей и большей ретроспективы (т.е. период рассмотрения статистических данных), что чаще всего невозможно реализовать. Число структурных элементов, участвующих в создании математической модели, было ограничено, что повлекло за собой констатацию существования такой таблично заданной зависимости (с ней имеет дело всякий медик-исследователь), которую нельзя аппроксимировать с помощью композиции выбранного набора элементов. Медицинские исследования обычно сталкиваются именно с такой ситуацией: задействовано большое количество параметров с таблично заданными значениями, а связь между ними явно не просматривается.
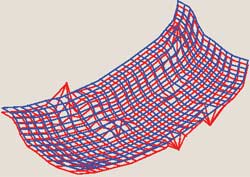
При использовании МГУА предполагается, что эту зависимость можно определить с помощью полинома Колмогорова — Габора [4]. Известно, что при увеличении его степени точность приближения функции возрастает, а потом убывает. В момент, когда точность максимальна, процесс усложнения полинома заканчивается. Число экспериментальных точек может быть значительно меньшим, чем число членов полинома, что является положительным моментом: медики редко располагают большим количеством экспериментальных данных, позволяющих достаточно точно отобразить процесс. На рис. 2 приводится примерное изображение функции, построенной с помощью МГУА (функция трех аргументов).
|
| Рис. 2. Аппроксимация функции с помощью МГУА («красный» — график реальной функции, синий — график полинома, полученного после применения МГУА) |
Для уменьшения количества комбинаций перебора необходимо использовать эмпирические процедуры. Число входных переменных определяется исследователем и ограничивается, в общем случае, мощностью компьютера. Отрицательным свойством этого метода с точки зрения его применения в медицине является то, что на сегодняшний день нет программного средства, позволяющего с помощью гибкого интерфейса получить сложную модель процесса. А значит, необходимо привлекать математиков с навыками программирования.
Как бы то ни было, сравнение результатов врачебного диагностирования патологий нервной системы с результатами, полученными с помощью логико-математических моделей на базе МГУА, показало, что использование таких моделей дает довольно точные результаты [5]. Этот метод также применялся американскими разработчиками для диагностирования раковых заболеваний, оценки умственных способностей людей и моделирования травматизма при дорожно-транспортных происшествиях.
Рассуждения на основе аналогичных случаев
РОАС — традиционный вариант принятия решения медиками, но проблема состоит в том, как хранить информацию по всем случаям, имевшим место в практике врача. Необходимы систематизация данных, выделение параметров и их значений для кодировки информации, чтобы в любой момент можно было извлечь требуемое описание. Причем данная информация, как правило, не имеет математического или даже числового выражения, позволяющего пользоваться перечисленными методами. А текстовую информацию, например описание реакции организма на различные раздражители или препараты, вообще далеко не всегда можно перевести в количественную. В таких случаях нужно обратиться к аппарату логики, который обеспечивает манипулирование лингвистическими (текстовыми) переменными.
Широкое применение получила нечеткая логика. В ее основе лежит представление о том, что составляющие множество элементы с общим свойством могут обладать им в различной степени, а следовательно, и принадлежать данному множеству с разной степенью. При таком подходе высказывания типа «случай относится к множеству случаев с диагнозом А» теряют смысл, поскольку необходимо указать, в какой степени случай принадлежит данному множеству.
Элементы нечеткого множества задаются не только в виде перечня, принятого в теории обычных множеств, но и в виде перечня пар (например, множеству А принадлежат члены Ai с функцией принадлежности (i). Высказывание врача «Я думаю, что у пациента на 80% злокачественная опухоль, а на 20% — доброкачественная» можно записать в виде нечеткого множества: «Диагноз пациента выбирается из множества диагнозов Д = {«Злокачественная опухоль»|0,8, «Доброкачественная опухоль|0,2}. Трудность задачи заключается в выборе элементов, входящих в множество, и в вычислении значения функции принадлежности. Максимальное значение функции принадлежности указывает на наибольшую значимость элемента, который она характеризует.
При обработке информации экспертной системой, построенной на основе рассуждений по правилам нечеткой логики, получится список диагнозов, с которыми соотносится степень принадлежности к ним описанного в запросе случая. Другими словами, при анализе имеющейся информации медик получит список, включающий в себя все возможные диагнозы, которые ставились при наличии всех выделенных для поиска симптомов.
Разработанная нами экспертная система в области терапевтической стоматологии, построенная на основе нечеткой логики, показала неплохой результат: 92% случаев с правильными диагнозами. При этом оставшиеся 8% нельзя считать ошибочными: это нетипичные случаи, которые входят в базу данных, но требуют более детального задания текста запроса за счет включения большего числа специфичных терминов. Эталоном правильности постановки диагноза считался диагноз, поставленный врачом, который предоставил информацию по конкретному случаю. Обучение системы проводилось на основе 11 892 случаев, а точность диагностирования проверялась с помощью контрольной выборки (5 тыс. случаев).
|
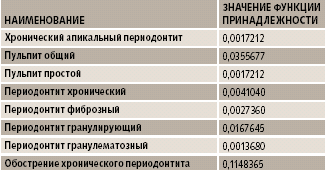
| Результат работы экспертной системы в виде списка диагнозов |
Результаты работы системы приведены в таблице. Исходный список диагнозов содержал 44 элемента, а после обработки системой сократился до 8. Окончательный диагноз выбирался из списка диагнозов с максимальным значением функции принадлежности.
Используя систему, медик может получить более полную картину заболевания, что поможет ему поставить диагноз. На основе информации экспертной системы можно наметить дальнейшие шаги, например определить, какие дополнительные анализы или осмотры нужно провести, чтобы получить новые аргументы в пользу того или иного диагноза. При грамотном построении информационной базы (оптимальном количестве вспомогательных полей, обеспечивающих максимальное быстродействие анализа и отсев неподходящих случаев) можно просматривать полные истории болезни даже нетипичных случаев, имевших место в практике врача или клиники.
Система прошла апробацию в одной из стоматологических поликлиник Краснодарского края и получила одобрение практикующих врачей. Она предложена для тестирования знаний при обучении медицинского персонала: на основе построенной базы знаний можно объективно подсчитывать баллы, набранные тестируемым. Планируется внедрение системы на кафедре терапевтической стоматологии Кубанской медицинской академии.
На пути к точным диагнозам
Наличие множества методов диагностики существенно затрудняет их выбор, от которого зависят точность и полнота получаемого результата. В случае необоснованного выбора может возникнуть впечатление, что вся работа проведена неудачно, но при всесторонней оценке типа и структуры информации часто удается подобрать метод, обеспечивающий хорошие результаты. Так, если информация имеет преимущественно численное выражение, то лучшие результаты покажут именно те методы, в которых используется математическое выражение изучаемого процесса. Если же данные имеют описательный характер, наилучшим способом окажется логическая обработка.
Описанная экспертная система не только позволяет точнее диагностировать заболевания, но и помогает в выборе курса лечения. Сейчас идет работа по повышению точности определения курса лечения. К сожалению, неизвестны факты промышленного применения в России аналогичных систем. Да и вообще, как отечественный, так и зарубежный опыт в данном отношении, к сожалению, не афишируется.
Литература
- Статистические методы исследования в медицине и здравоохранении / Под ред. Л.Е. Полякова. — Л.: Медицина, 1971.
- Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере. / Новосибирск: Наука, 1996.
- Baxt W.G. Use of an artificial neural network for the diagnosis of myocardial infarction. / Ann. Intern. Med. 1991, Vol. 115, Nо. 11.
- Ивахненко А.Г., Лапа В.Г. Предсказание случайных процессов. / Киев: Наукова думка, 1971.
- Сироджа И.Б. Квантовые модели и методы искусственного интеллекта для принятия решений и управления, Киев: Наукова думка, 2002.
Рената Поповьян (renata1605@inbox.ru) — ИТ-специалист Апшеронской районной стоматологической поликлиники (г. Апшеронск).


